.
Arboles y Recursividad
Decimos que una definición es recursiva cuando "define en función de si misma". Un algoritmo es recursivo cuando para resolver el problema se invoca a si mismo una y otra vez hasta resolverlo.
Para comprender esto lo mejor será analizar algunos casos típicos como la función matemática factorial.
Definimos la función factorial de la siguiente manera: Sea x perteneciente al conjunto de los números naturales (incluyendo al cero) entonces:
- factorial(x) = x*factorial(x-1)
- factorial(0) = 1
Desde el punto de vista de la programación, programar esta función recursiva no implica ni más ni menos que seguir al pie de la letra su definición matemática.
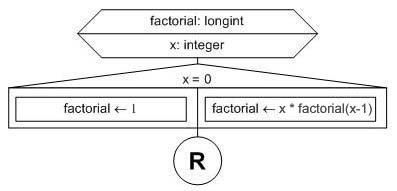
Como vemos, la función recibe un parámetro x. Si x es igual a 0 entonces retorna 1. Si x es mayor que cero entonces retorna el producto de x por "lo que retorna la misma función" invocándola con el parámetro (x-1).
A continuación vemos un programa principal que lee un valor n y muestra el factorial de n utilizando la función recursiva.
En Pascal, lo anterior se codifica de la siguiente manera:
testFactorial.pas
1:
2:// funcion factorial recursiva
3:function factorial(x: integer): longint;
4:begin
5: if( x=0 ) then begin
6: factorial:=1;
7: end else begin
8: factorial:=x*factorial(x-1);
9: end;
10:end;
11:
12:// programa principal
13:var n: integer;
14:begin
15: write('Ingrese un valor: ');
16: read(n);
17: write('El factorial de ',n,' es: ');
18: writeln( factorial(n) );
19:end.
20:
Notemos que la función factorial puede resolverse también sin necesidad de utilizar recursividad. De hecho, ese fue uno de los primeros ejemplos que analizamos en este este trabajo.
Si bien el algoritmo es bastante simple, esta versión resulta más compleja que la versión recursiva.
Pila de Llamadas
Para comprender bien el funcionamiento de los procedimientos y las funciones recursivas es fundamental notar que cada llamada (o invocación) a un procedimiento o función queda apilada en una "pila de llamadas" de forma tal que cada procedimiento o función que se encuentre apilado no podrá finalizar su ejecución si antes no finalizaron los procedimientos y/o funciones que fueron llamados (apilados) con posterioridad.
Para hacerlo más simple, si en la función f invocamos a la función g y en la función g invocamos a la función h entonces la primer función en finalizar su ejecución será h, luego g y por último f. Y cuando finalice h, la función g continuará su ejecución exactamente en la línea siguiente a la llamada a la función h. Y cuando finalice g, f continuará su ejecución en la línea siguiente a la llamada a g.
Cuando tenemos el caso de una función recursiva, cada invocación recursiva (a si misma) será apilada en la pila de llamadas, así que la invocación a la función no terminará hasta que no terminen las invocaciónes que fueron apiladas posteriormente.
Esto lo podemos probar con el siguiente ejemplo:
testRecursivo.pas
1:
2:// procedimiento recursivo
3:procedure miProcRecursivo(n:integer);
4:begin
5: writeln('comienza (n=',n,')');
6: if( n<4 ) then begin
7: miProcRecursivo(n+1);
8: end;
9: writeln('finaliza (n=',n,')');
10:end;
11:
12:// programa principal
13:begin
14: miProcRecursivo(1);
15:end.
16:
En este programa vemos un procedimiento llamado miProcRecursivo que recibe un parámetro numérico. Lo primero que hace es decir "Comienza" y mostrar el valor del parámetro que recibe. Luego se invoca a si mismo solo si el parámetro recibido es menor que 4. Cuando se invoca a si mismo se pasa como parámetro n+1 por lo que si había recibido un valor de n igual a 1, la llamada siguiente (recursiva) recibirá un valor de n igual a 2. Por último, antes de terminar muestra un mensaje diciendo "Finaliza" con el valor del parámetro n que recibió.
En el programa principal invocamos al procedimiento pasándole como parámetro el valor 1. La salida será la siguiente:
La salida muestra la pila de llamadas: se llamó al procedimiento con el parámetro 1, luego con 2, luego con 3, luego con 4. El primero en finalizar fue el que recibió el parámetro 4, luego el 3, luego el 2, luego el 1. "El último que se llamó fue el primero que finalizó".
Es muy importante notar que la función recursiva debe tener una condición de corte. En este ejemplo la condición de corte
es if( n < 4 ). Si no estuviese esta condición entonces el procedimiento se llamaría a si mismo permanentemente trayendo aparejadas dos consecuencias: primero el programa se colgaría ya que nunca retornará el control al programa principal y, segundo, dado que la pila de llamadas se implementa en memoria, en algún momento la memoria libre se acabará y tendremos un error llamado "stack overflow" que hará finalizar abruptamente la ejecución del programa.
Vamos a probarlo:
testRecursivo2.pas
1:
2:// procedimiento recursivo
3:procedure miProcRecursivo(n:integer);
4:begin
5: writeln('comienza (n=',n,')');
6:
7: // invocamos recursivo siempre, sin condicion
8: miProcRecursivo(n+1);
9:
10: // nunca se llega a este punto
11: writeln('finaliza (n=',n,')');
12:end;
13:
14:// programa principal
15:begin
16: miProcRecursivo(1);
17:end.
18:
El resultado es:
El programa corta abruptamente tirando un "Runtime error 202". El código de error 202 indica que ocurrió un "Stack Overflow" (desbordamiento de la pila). Y, de hecho, lo que muestra en la consola (pantalla) es el "Stack Trace": estado de la pila de llamadas al momento de ocurrir el error.
Volviendo a la función recursiva factorial ahora podemos notar que la condición de corte es if( x=0 ).
Problema 8.1
Se tiene el archivo EMPLEADOS.dat con la información de cada empleado de la compañia.
EMPLEADOS.dat
- id - (integer)
- nombre - (string[40])
- idJefe - (integer, hace referencia al id del jefe del empleado)
El "gerente general" de la compañia, también figura como empleado y su idJefe será -1.
Se pide desarrollar un programa interactivo que permita ingresar el id de un empleado y luego imprima toda la línea jerárquica a la cual responde el empleado cuyo id se ingresó.
Análisis
El problema se resuelve muy facilmente utilizando un procedimiento recursivo que llamaremos imprimirJefe.
Comencemos por definir la sección type para luego analizar el programa principal en el que haremos la invocación al procedimiento recursivo.
1:
2:type
3: REmpleado = record
4: id: integer;
5: nombre: string[40];
6: idJefe: integer;
7: end;
8:
9: FEmpleados = file of REmpleado;
10:
Ahora veamos el programa principal.
El programa principal es verdaderamente simple. Leemos el id del empleado a consultar y accedemos al archivo para averiguar su nombre y su jefe directo (idJefe). Imprimimos los títulos e invocamos al procedimiento imprimirJefe para que haga el resto del trabajo.
Para acceder al archivo desarrollamos el procedimiento leer que recibe el id de un empleado y realiza el acceso directo y la lectura sobre el archivo. La información leida queda almacenada en el parámetro (por referencia) reg.
Notemos que a imprimirJefe lo estamos invocando con el parámetro reg.idJefe por lo tanto el procedimiento debe mostrar el nombre de este empleado (el jefe del empleado que originó la consulta) e invocarse a si mismo con el id de su jefe ("el jefe del jefe"). Así hasta que el empleado no tenga jefe.
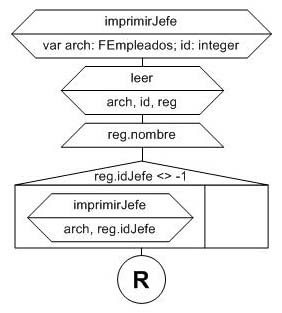
El procedimiento imprimirJefe recibe el id de un empleado, accede al archivo para recuperar su nombre (reg.nombre) y el id de su jefe (reg.idJefe). Muestra el nombre del empleado recibido y (si tiene jefe) se llama a si mismo pasándo como parámetro el id del jefe.
imprimirJefe es un procedimiento recursivo ya que resuelve su tarea invocándose a si mismo.
Problema 8.2
Se tiene el archivo FAMILIAS.dat con la información de un conjunto de familias, con el siguiente formato.
FAMILIAS.dat
- nombre - string[30]
- cantHijos - integer
En el ejemplo vemos reflejados los datos de 3 familias:
La familia de "Juan" tiene dos hijos: "Maria" (no tiene hijos) y "Carlos", que tiene un hijo: "Ezequiel" quien tiene dos hijos: "Martín" y "Romina" ambos sin hijos.
La familia de "Alberto" (quien no tiene familia ya que no tiene hijos).
La familia de "Marcelo" quien tiene un hijo: "Gerardo" quien tiene dos hijos: "Silvana" y "Karina" ambas sin hijos.
Se pide hacer un programa que imprima un listado de todas las familias registradas en el archivo indicando el nombre del pariente más viejo (en el ejemplo serían "Juan", "Alberto" y "Marcelo") y la cantidad de integrantes que tiene cada familia (sumatoria de hijos, nietos, etc)
Análisis
Para resolver este problema vamos a pensar en una función que llamaremos leerFamilia. Esta función retornará true o false según haya podido procesar correctamente los datos de una familia del archivo. Si retorna true, en los parámetros de salida retornará el nombre y la cantidad de integrantes de la familia que procesó.
Con esta función (que luego analizaremos en detalle) el programa principal queda resuelto de la siguiente manera.
En el programa principal abrimos el archivo y simplemente iteramos mientras la función tenga datos para procesar. Es decir: iteramos mientras la función retorne true. La misma función se encarga de asignar el nombre y la cantidad de miembros en las variables nomFlia y totMiembros por lo que en el programa principal simplemente mostramos sus contenidos para generar el listado que se pide en el enunciado.
La función se ocupa de recorrer el archivo por lo tanto debe controlar que no llegue el eof. Retorna true o false si leyó un registro y (en ese caso) asignó valores a los parámetros suma y nomFlia. Recordemos que al leer el último registro de un archivo la función eof retorna true por este motivo el if( eof(arch) ) lo hacemos al comienzo de la función y si retorna true entonces finalizamos la función retornando false (no hay más registros por leer).
Basicamente la función lee un registro (una persona), obtiene la cantidad de hijos de esta persona y luego entra en un for donde se llama a si misma tantas veces como hijos tiene la persona que leyó.
Dentro del for se incrementa la variable suma (parámetro que recibe por referencia) por lo tanto, si la persona leida tiene tres hijos, el for iterará tres veces y la suma se incrementará en 3, pero a su vez, dentro del for se invoca a la función pasándole la misma variable suma por lo que si uno de los hijos de la persona leida tiene 5 hijos más, la llamada recursiva incrementará la (misma) variable suma otras cinco veces, y así.
Notemos también que antes de ingresar al for preguntamos si suma es cero. En este caso estaremos ante la presencia de un "jefe de familia", entonces asignamos su nombre al parámetro nomFlia. Justamente la variable suma (que en el programa principal es totMiembros) se inicializa en cero antes de invocar a la función.
familias.pas
1:
2://
3:// seccion type
4://
5:type
6: RFamilia = record
7: nombre: string[30];
8: cantHijos: integer;
9: end;
10:
11: FFamilias = file of RFamilia;
12:
13:
14://
15:// funcion leerFamilia
16://
17:function leerFamilia(var arch: FFamilias
18: ; var nomFlia:string[30]
19: ; var suma: integer): boolean;
20:var
21: reg: RFamilia;
22: nomFliaAux: string[30];
23: i: integer;
24:
25:begin
26: // si no hay mas datos en el archivo retorna false
27: if( eof(arch) ) then begin
28: leerFamilia:=false;
29: exit; // la funcion finaliza aqui...
30: end;
31:
32: // leo un registro
33: read(arch,reg);
34:
35: // si suma es cero entonces es un "jefe" de flia
36: if( suma=0 ) then begin
37: nomFlia:=reg.nombre;
38: end;
39:
40: // itero tantas veces como hijos tiene la persona
41: for i:=1 to reg.cantHijos do begin
42:
43: suma:=suma+1; // incremento una vez por hijo
44:
45: // invoco recursivamente a la funcion para
46: // procesar los hijos de los hijos
47: leerFamilia(arch,nomFlia,suma);
48:
49: end;
50:
51: // la funcion returna true porque pudimos asignar
52: // datos a los parametros nomFlia y suma
53: leerFamilia:=true;
54:end;
55:
56:
57://
58:// programa principal
59://
60:
61:var
62: arch: FFamilias; reg: RFamilia;
63: nomFlia: string[30];
64: totMiembros:integer;
65:begin
66: // abro el archivo
67: assign(arch,'FAMILIAS.dat');
68: reset(arch);
69:
70: // inicializo la variable en la cual la funcion
71: // sumara los miembros de cada familia
72: totMiembros:=0;
73:
74: // cada iteracion corresponde a una nueva familia
75: while( leerFamilia(arch,nomFlia,totMiembros) )
76: do begin
77: // imprimo una linea del listado
78: writeln( nomFlia, ' ',totMiembros );
79:
80: // reseteo la variable
81: totMiembros:=0;
82: end;
83:
84: // cierro el archivo
85: close(arch);
86:end.
87:
Arboles
Los árboles son estructuras de datos recursivas. Esto es: nodos que tienen 2 o más punteros a nodos de su mismo tipo. Al representarlos graficamente vemos que tienen forma de árbol.
El árbol tiene una raíz la cual tiene dos o más ramas. Cada rama es en sí misma una raíz con más ramas y así, por lo tanto para recorrer un árbol necesitaremos un algoritmo recursivo.
Según la cantidad de hijos que tengan sus nodos, los árboles se clasifican en árboles binarios (2 hijos), árboles ternarios (3 hijos) o árboles n-arios (n hijos, con n variable).
El diagrama anterior representa un árbol binario.
En este capítulo trabajaremos con árboles binarios. Luego, en los ejercicios explicaremos otros casos a medida que se vayan planteando.
Definición del Nodo del Arbol Binario
1:
2:type
3: PNArbol = ^NArbol;
4: NArbol = record
5: info: integer;
6: izq: PNArbol; // puntero al hijo izquierdo
7: der: PNArbol; // puntero al hijo derecho
8: end;
9:
Ahora consideraremos un conjunto de valores numéricos, sin ningún orden como podría ser el conjunto A que veremos a continuación:
A = { 5, 2, 8, 9, 1, 4, 6, 3, 7 }
Con los valores de este conjunto analizaremos las diferentes operaciones que podemos aplicar a los árboles.
Agregar Nodos a un Arbol Binario
Pensemos en un programa que cargue los datos del conjunto en un árbol binario con el siguiente criterio: "los valores menores van a la izquierda, los valores mayores van a la derecha".
Respetando este criterio, si se agregan los valores del conjunto A en en su orden original, el árbol que los contenga se verá de la siguiente manera:
El primer valor es el 5, por lo tanto será la raíz del árbol. Luego ingresa un 2. Como es menor que 5 lo ubicamos en el nodo izquierdo. Luego ingresa 8, que es mayor que 5 así que lo ubicamos en su nodo derecho. A continuación ingresa 9, es mayor que 5, pasamos a su nodo derecho que tiene 8, como 9 es mayor que 8 lo ubicamos en su nodo derecho. Luego llega el 1 que es menor que 5. Vemos su nodo izquierdo y encontramos al 2. Como 1 es menor que 2 lo ubicamos en su nodo izquierdo, y así hasta cargar todos los datos del conjunto.
1:
2:// programa principal
3:var raiz: PNArbol;
4:begin
5: agregarValor(raiz,5);
6: agregarValor(raiz,2);
7: agregarValor(raiz,8);
8: agregarValor(raiz,9);
9: agregarValor(raiz,1);
10: agregarValor(raiz,4);
11: agregarValor(raiz,6);
12: agregarValor(raiz,3);
13: agregarValor(raiz,7);
14: // :
15:end.
16:
Veamos ahora el procedimiento agregarValor que se ocupa de agregar nodos al árbol respetando el criterio indicado.
1:
2:procedure agregarValor(var raiz: PNArbol; v: integer);
3:begin
4: // si la raiz es nula entonces le asigno memoria
5: // guardo la informacion (v) y finalizo el proc.
6: if( raiz = NIL ) then begin
7: new(raiz);
8: raiz^.info:=v;
9: raiz^.der:=NIL;
10: raiz^.izq:=NIL;
11: exit;
12: end;
13:
14: // si estoy aca es porque la raiz no es NIL
15: // entonces si el valor v que vamos a agregar es
16: // menor que el valor de la raiz vuelvo a invocar
17: // al procedimiento considerando como raiz
18: // al hijo izquierdo. Si es mayor o igual lo
19: // invoco considerando al hijo derecho
20: if( v < raiz^.info ) then begin
21: agregarValor(raiz^.izq, v );
22: end else begin
23: agregarValor(raiz^.der, v );
24: end;
25:end;
26:
Al cargar el árbol siguiendo este criterio decimos que el árbol es un arbol binario de búsqueda. Es decir que podemos utilizar un árbol binario para realizar búsquedas con la misma eficiencia que una búsqueda binaria y también podemos utilizarlo para ordenar conjuntos.
Veremos que según el recorrido que realicemos sobre sus nodos, los valores (en este caso numéricos) resultarán ordenados ascendentemente.
Recorrer los nodos del Arbol
Recorrido de Orden Inverso (o inOrden): Este recorrido consiste en "bajar" por la rama izquierda hasta el último nodo, listar su valor, subir un nivel, listar el valor del padre y considerar al hijo derecho como nueva raiz para repetir la operación.
En nuestro ejemplo: "bajamos" por la rama izquierda hasta llegar al último nodo, que contiene el valor 1. Listamos su valor (1) y luego "subimos" un nivel para listar el valor del padre (2). Ahora repetimos la operación con el hijo derecho: "bajamos" hasta el último nodo. Listamos su valor (3). Subimos un nivel y listamos el padre (4). Repetimos la operación con su hijo derecho (que en este caso no tiene) entonces subimos otro nivel (que ya fue procesado, el 2), subimos otro nivel y listamos el (5) para luego bajar a su hijo derecho y repetir toda la operación bajando hasta el último nodo por la izquierda (6) y así sucesivamente hasta terminar.
Si analizamos la salida de este recorrido (los núneros en rojo) veremos que fueron saliendo en orden.
Por lo tanto, si tenemos un árbol binario de búsqueda al recorrerlo con "orden inverso" lo veremos ordenado.
El código para un recorrido de orden inverso es el siguiente:
1:
2:procedure inOrden(raiz: PNArbol);
3:begin
4: if( raiz<>NIL ) then begin
5: inOrden(raiz^.izq);
6: writeln( raiz^.info);
7: inOrden(raiz^.der);
8: end;
9:end;
10:
Basicamente lo que hace este procedimiento es llamarse a si mismo con el hijo izquierdo y terminar si es NIL.
Hagamos un seguimiento con los datos del ejemplo que estamos analizando.
Invocamos al procedimiento pasándole un puntero a la raíz del árbol: 5. Como es distinto de NIL se llama a si mismo con su hijo izquierdo: 2, que como es distinto de NIL se llama a si mismo con su hijo izquierdo: 1, que como es distinto de NIL se llama a si mismo con su hijo izquierdo: NIL. Esta útima llamada finaliza sin hacer nada ya que no ingresa al if. Así que regresamos a la llamada anterior (la del 1). Imprime su valor (1) y se llama a si mismo con su hijo derecho quien es NIL por lo tanto finaliza. En este momento finaliza la invocación al procedimiento con el valor 1, así que regresamos a la llamada anterior: imprime el (2) y se llama a si misma con su hijo derecho: 4 que como es distinto de NIL se llama a si misma con su hijo izquierdo: 3, y así sucesivamente.
Recorrido de PreOrden: Este recorrido considera primero la raíz, luego el arbol izquierdo y por último el arbol derecho.
En preOrden, los nodos de nuestro árbol se listarían de la siguiente manera:
5, 2, 1, 4, 3, 8, 6, 7, 9
El algoritmos para recorrerlo en este orden es el siguiente:
1:
2:procedure preOrden(raiz: PNArbol);
3:begin
4: if( raiz<>NIL ) then begin
5: writeln( raiz^.info);
6: preOrden(raiz^.izq);
7: preOrden(raiz^.der);
8: end;
9:end;
10:
Primero imprimimos, luego invocamos con el hijo izquierdo y luego con el hijo derecho.
Recorrido de Orden Posterior (o postOrden): este recorrido implica recorrer primero la rama izquierda, luego la derecha y por último procesar la raíz.
En nuestro ejemplo, el recorrido postOrden arrojará el siguiente resultado:
1, 3, 4, 2, 7, 6, 9, 8, 5
y el algoritmos para procesarlo es el siguiente:
1:
2:procedure postOrden(raiz: PNArbol);
3:begin
4: if( raiz<>NIL ) then begin
5: postOrden(raiz^.izq);
6: postOrden(raiz^.der);
7: writeln( raiz^.info);
8: end;
9:end;
10:
Algoritmos y Estructuras de Datos
UBA UTN FRBA
.













