Problema 3.3

.
Enunciado
1 - Desarrollar un programa que indique si un número (ingresado por teclado) es número primo o no.

2 - Desarrollar un programa que muestre por pantalla los primeros n números primos. El valor n se ingresa por teclado.


Análisis
Un número es primo si solo es divisible por si mismo y por la unidad. Es decir, los números que no admiten divisores salvo ellos mismos y la unidad son primos.

Números primos son (por ejemplo) 1, 2, 3, 5, 7, 11, 13, 17, etc... Todos estos números solo pueden dividirse por 1 y por ellos mismos.

Los dos problemas son (en si mismos) muy simples. La única complejidad que tienen es común a ambos: determinar si un número es primo o no.

Supongamos que contamos con una función llamada esPrimo que recibe un valor numérico entero y retorna true o false según ese valor sea o no número primo. Contando con esta función los problemas se resuelven de la siguiente manera:

Vemos la solución del problema 1. Simplemente leemos un valor e invocamos a la función esPrimo pasándole el valor leido. Si retorna true entonces mostramos un mensaje indicando que el número es primo. Si retorna false mostramos un mensaje diciendo que no lo es.

Vemos la solución del problema 2.

Tenemos que mostrar tantos números primos como indique el valor de la variable n. La solución será tener un contador de números primos (contPrimos) y una variable i que se incremente desde 1 en adelante. Por cada valor de i invocamos a la función esPrimo. Si retorna true entonces mostramos i e incrementamos contPrimos ya que encontramos un número primo más. Así hasta que contPrimos llegue a la cantidad de números primos deseada, ingresada por el usuario (n).

Ahora analicemos la función esPrimo.

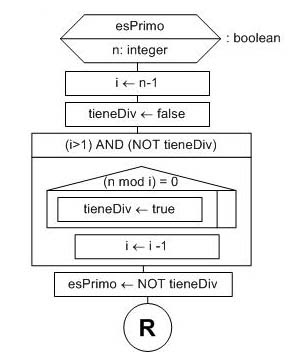
La estrategia es la siguiente: para saber si un número n es primo o no tendremos una variable i inicializada en n-1 que se decrementará mientras no llegue a 1. Luego, por cada uno de sus valores calculamos el resto en la división de n por i haciendo n mod i. Si el resto es cero entonces i es divisor de n. Como el número n tiene divisores retornamos false ya que no es primo. En cambio, si no tiene divisores retornamos true porque es primo.


Ahora bien, tenemos dos programas diferentes que utilizan la misma función. Para que esto pueda ser posible la función debe estar en un archivo .pas separado, en una unit.

untPrimos.pas

   1:
   2:unit untPrimos;
   3:
   4:interface
   5:
   6:   // retorna true o false segun el numero n
   7:   // sea primo o no
   8:   function esPrimo(n: integer):boolean;
   9:
  10:implementation
  11:
  12:function esPrimo(n: integer):boolean;
  13:var i:integer; tieneDiv: boolean;
  14:begin
  15:
  16:   // con i probaremos cada uno de los numeros
  17:   // entre n y 1 para ver si alguno es divisor de n
  18:   // por eso i comienza en n-1
  19:   i:=n-1;
  20:
  21:   // de entrada considero que el numero
  22:   // no tiene divisores
  23:   tieneDiv:=false;
  24:
  25:   // itero mientras i no llegue a 1 y mientras
  26:   // no encuentre ningun divisor
  27:   while( (i>1) AND (NOT tieneDiv) ) do begin
  28:
  29:      // si i es divisor de n
  30:      if( (n mod i) = 0 ) then begin
  31:         tieneDiv:=true;
  32:      end;
  33:      i:=i-1;
  34:   end;
  35:
  36:   // si n tiene divisores entonces retorno 
  37:   // false (no es primo), si n no tiene
  38:   // divisores entonces retorno true (es primo)
  39:   // es decir: retorno la negacion de tieneDiv
  40:   esPrimo:= (NOT tieneDiv);
  41:end;
  42:end.
  43:

Veamos ahora el código de los problemas 1 y 2.

primos1.pas

   1:
   2:uses untPrimos;
   3:
   4:var num:integer;
   5:begin
   6:   write('Ingrese un valor: ');
   7:   readln(num);
   8:
   9:   // invocamos a la funcion esPrimo y segun lo
  10:   // que retorne mostramos el mensaje
  11:   if( esPrimo(num) ) then begin
  12:      writeln(num,' es primo');
  13:   end else begin
  14:      writeln(num,' no es primo');
  15:   end;
  16:end.
  17:

primos2.pas

   1:
   2:uses untPrimos;
   3:var n,contPrimos,i:integer;
   4:begin
   5:   write('Ingrese un valor: ');
   6:   readln(n);
   7:
   8:   // contador de numeros primos que vamos mostrando
   9:   contPrimos:=0;
  10:
  11:   i:=1;
  12:
  13:   // mientras no hayamos mostrado la cantidad de
  14:   // numeros primos que nos pide el usuario
  15:   while( contPrimos<n ) do begin
  16:
  17:      // si el valor de i (que comienza desde 1)
  18:      // es primo...
  19:      if( esPrimo(i) ) then begin
  20:
  21:         // muestro i
  22:         writeln(i);
  23: 
  24:         // incremento el contador de numeros primos
  25:         contPrimos:=contPrimos+1;
  26:      end;
  27:
  28:      // incremento i para probar si el siguiente
  29:      // entero es primo
  30:      i:=i+1;
  31:   end;
  32:end.
  33:

.