..
Arrays
Un array es un conjunto de variables del mismo tipo cuyas direcciones de memoria son consecutivas. Por lo tanto se puede identificar a cada una de las variables del conjunto con un subíndice.
Veamos un ejemplo.
testArray.pas
1:
2:var arr: array [1..5] of integer;
3:begin
4: arr[1]:=2;
5: arr[2]:=4; // asigno el valor 4 en la posicion 2
6: arr[3]:=6;
7: arr[4]:=8; // asigno el valor 8 en la posicion 4
8: arr[5]:=10;
9:
10: // imprimo el valor de cada elemento del array
11: writeln('valor de arr[1]=',arr[1]);
12: writeln('valor del arr[2]=',arr[2]);
13: writeln('valor del arr[3]=',arr[3]);
14: writeln('valor del arr[4]=',arr[4]);
15: writeln('valor del arr[5]=',arr[5]);
16:end.
17:
En el programa anterior definimos una variable arr de tipo array [1..5] of integer. Es decir: definimos un array de enteros, de 5 elementos. Luego le asignamos un valor entero a cada una de los elementos del array y (por último) mostramos los valores que contienen los elementos de cada una de las posiciones.
Veamos una representación gráfica del array arr.
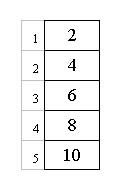
Vemos en la columna principal (recuadrada con líneas negras) las celdas que representan cada uno de los elementos del array y sus respectivos valores. Y en la columna de la izquierda (con líneas grises) los subíndices que representan las posiciones de cada uno de los elementos.
La posibilidad de acceder a los elementos del array referenciándolos mediante un subíndice es fundamental y hace de los arrays un recurso indispensable para la resolución de cierto tipo de problemas.
Modifiquemos el programa testArray.pas para acceder automaticamente a las posiciones del array mediante el uso de ciclos for.
testArray2.pas
Con el primer for cargamos el array. El for itera haciendo variar i entre 1 y 5. Por lo tanto en la primer iteración, cuando i vale 1 hablar de arr[i] es hablar de arr[1]. En la siguiente iteración i valdrá 2 entonces hablar de arr[i] es hablar de arr[2] y así.
Asignamos arr[i] := 2*i ya que (siguiendo con el ejemplo anterior) lo que queremos asignar en cada posición coincide con "el doble del índice" de cada posición del array.
Con el segundo for recorremos el array y mostramos lo que contiene en cada una de sus posiciones.
Es muy importante tener en cuenta que los arrays son estructuras de datos estáticas. Se definen antes de que comience a ejecutarse el algoritmo por lo tanto tenemos que definir de antemano su longitud (cantidad de elementos).
No podemos hacer esto:
Definir un array de (por ejemplo) 10 elementos no implica que (luego) necesariamente vayamos a utilizar esos 10 elementos. Podemos utilizar solo algunos o (a lo sumo) los 10. Obviamente, aunque solo utilicemos 1 de los 10 elementos del array la memoria reservada siempre será de 10 elementos durante toda la ejecución del programa.
Operaciones Sobre Arrays
Buscar, insertar, eliminar y ordenar elementos sobre un array son algunas de las operaciones que vamos a estudiar en este capítulo.
Analizaremos los siguientes procedimientos y funciones que definiremos en una unit.
untArray.pas
Notemos que todos los procedimientos y funciones reciben el parámetro len. Este parámetro indica la cantidad de elementos útiles del array. Es decir, si tenemos un array de 10 posiciones de las cuales hasta el momento ninguna está siendo utilizada entonces el valor del parámetro len será 0. Pero si en ese mismo array insertamos un valor entonces el parámetro len debe pasar a valer 1 ya que en el array ahora tenemos 1 elemento útil (y espacio libre para nueve elementos más que hasta el momento no están siendo utilizados).
procedure insertar (implementación)
El objetivo de este procedimiento es insertar un valor (valor) en una posición (pos) del array (arr) desplazando hacia abajo todos los elementos que se encuentran a partir de la posición pos inclusive.
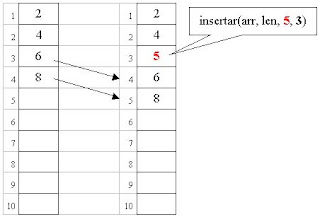
En el gráfico vemos como queda el array luego de insertar el valor 5 en la posición 3. El valor que estaba en la posicion 4 pasó a la posición 5 y el valor que estaba en la posición 5 pasó a la posición 6.
Es importante notar como juega el valor del parámetro len. El parámetro len indica cuantas posiciones del array están siendo efectivamente utilizadas. En el primer caso el parámetro len vale 4 ya que el array contiene 4 elementos. El procedimiento insertar debe incrementar el valor del parámetro len para reflejar que (luego de insertar el nuevo elemento) el array tiene un elemento más.
Notemos que el array tiene una longitud de 10 elementos. Sin embargo no todos necesariamente tienen que ser utilizados. Justamente eso es lo que refleja el parámetro len. Los elementos útiles del array son los que están en las posiciones 1 a len.
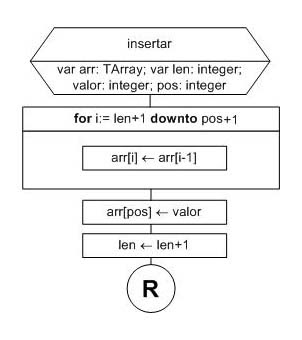
Análisis
Utilizamos un for downto que comienza en len+1 y termina en pos+1.
Considerando el ejemplo anterior, tendremos: len=4 (entonces len+1=5) y pos=3 (o sea que pos+1=4). El for itera con i variando entre 5 y 4. En la primera vuelta (i vale 5) a arr[5] le asignamos arr[4]. En la próxima vuelta (i vale 4) a arr[4] le asignamos arr[3]. Luego asignamos valor a arr[pos].
Desplazamos todos los elementos hacia abajo para poder insertar el nuevo valor en la posición pos.
untArray.pas (implementación: procedure insertar)
Con esto podemos resolver el siguiente problema.
Problema 5.1
Dado un conjunto de valores positivos (no serán más de 10 valores) imprimirlo en orden inverso. Fin de datos: valor negativo.
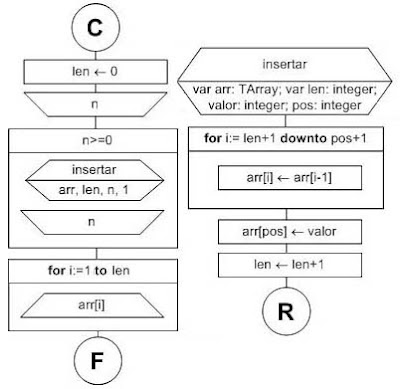
Análisis
Leemos valores mientras no se ingrese un valor negativo y los insertamos en el array arr, en la posición 1. Todos los insertamos en la primer posición.
Supongamos que los valores que ingresan son: { 3, 2, 1, -1 } entonces la secuencia será la siguiente.
Insertamos el 3 en la posicion 1. Luego insertamos el 2 en la posición 1 (desplazando el 3 a la posición 2). Luego insertamos el 1 en la posición 1 (desplazando el 2 a la posición 2 y el 3 a la posición 3). Así, al momento de recorrer e imprimir el array la salida será: 1, 2, 3.
Recordemos que el procedimiento insertar incrementa el valor del parámetro len cada vez que inserta un valor en el array.
problema5.1.pas
procedure eliminar (implementación)
El objetivo de este procedimiento es eliminar el valor contenido en una posición del array desplazando una posición hacia arriba todos los elementos que se encuentren en las posiciones siguientes.
Análisis
La solución para este algoritmo es simple. Asignar en la posición pos el elemento de la posición pos+1. Luego asignar en la posición pos+1 el elemento de la posición pos+2, y así, si hacemos variar a i entre pos y len-1 podemos asignar al array arr en la posición arr[i] el elemento de la posición arr[i+1].
Por último, la cantidad de elementos útiles del array decreció. Entonces tenemos que decrementar el valor del parámetro len (que recibimos por referencia).
untArray.pas (implementación: procedure eliminar)
function buscar (implementación)
Este algoritmo lo implementamos como una función. El objetivo es buscar un elemento en el array. El elemento puede estar o no. Si el elemento está entonces la función retorna la posición en la cual se encontró el elemento. Si el elemento no está entonces la función retorna -1 para indicar que el elemento no se encontró en el array.
Análisis
Recorremos el array mientras no nos pasemos de la última posición (len) y mientras no encontremos el elemento que buscamos.
Cuando corta el while preguntamos por cual de las dos condiciones cortó. si cortó porque i es mayor que len entonces llegamos al final y no encontramos el elemento. Retornamos -1. Si cortó porque arr[i] = valor entonces lo encontró en la posición i. Retornamos el valor de i.
untArray.pas (implementación: function buscar)
Problema 5.2
Leer un conjunto A de valores positivos (finaliza con un valor negativo). Luego leer otro conjunto B de valores positivos (finaliza con un valor negativo). Imprimir los valores del conjunto A que no pertenezcan al conjunto B. Se garantiza que los conjuntos no tendrán más de 10 valores.
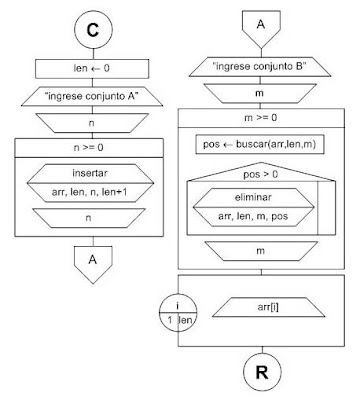
Análisis
Leemos los valores del conjunto A y los insertamos en el array arr, en la posicion len+1 (es decir: siempre al final).
Luego leemos los valores del conjunto B y por cada valor buscamos en el array. Si se encuentra entonces lo eliminamos del array.
Por último, recorremos e imprimimos los elementos de arr que serán los elementos del conjunto A que no pertencen al conjunto B.
problema5.2.pas
function insertarOrdenado (implementación)
El objetivo de esta función es insertar un elemento (valor) en el array (arr) pero considerando un orden de precedencia. Luego retorna la posición en la cual se insertó el elemento.
Análisis
Recorremos el array mientras no nos pasemos del último elemento útil (len) y mientras no encontremos un elemento mayor que el valor que nos piden insertar (valor). Cuando corta el while preguntamos por cual de las dos condiciones cortó. Si corto porque i es mayor que len entonces el array no contiene ningún elemento menor o igual que valor. Es el mayor y debemos insertarlo al final.
Si el while cortó porque arr[i] es mayor que valor entonces tenenos que insertar el elemento en la posición i. Llamamos al procedimiento insertar y retornamos el valor de i.
untArray.pas (implementación: function insertarOrdenado)
function buscarEInsertarOrdenado (implementación)
Esta función es similar a la anterior. La diferencia es que antes de insertar el elemento verifica si ya existe en el array. Si ya existe entonces no lo inserta y devuelve la posición donde lo encontró. Si no existe entonces lo inserta respetando el orden de precedencia y retorna la posición donde lo insertó. Para indicar al usuario (quien llama a la función) si el elemento existía previamente o si lo tuvo que insertar, la función retorna su valor en positivo o en negativo. Es decir:
A medida que vamos teniendo más funciones resueltas resulta más facil programar nuevas funciones.
Para resolver esta función primero buscamos el elemento valor. Si no lo encontramos entonces lo insertamos ordenado. En ret tenemos la posición donde se insertó el elemento pero la tenemos que negativizar para retornar ese mismo valor en negativo. De esta manera le indicamos al llamador (programa que invoca a esta función) que el elemento no estaba y entonces lo insertamos.
Si el elemento fue encontrado entonces simplemente retornamos la posición en la que se encontró.
untArray.pas (implementación: function buscarEInsertarOrdenado)
Problema 5.3
Leer un conjunto de valores e imprimirlos ordenados, sin repetición. El conjunto finaliza con un valor cero. No tendrá más de 10 valores. Indicar cuantos valores repetidos tiene el conjunto.
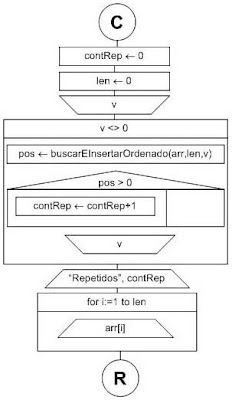
Análisis
El problema es muy simple. Leemos los valores del conjunto mientras no se ingrese el elemento final identificado por un valor cero. Tenemos un array arr en el cual buscamosEInsertamos los valores del conjunto. Es decir: solo insertamos si no existen previamente. Los que se repiten los podemos identificar porque la función buscarEInsertarOrdenado los encontrará en el array y retornará un valor positivo entonces en contRep contamos la cantidad de valores repetidos del conjunto. Al finalizar el ingreso de datos, el array contendrá todos los elementos no repetidos del conjunto y estos estarán ordenados.
problema 5.3.pas
Problema 5.4
Un kiosco vende 100 artículos diferentes. Al finalizar el día de trabajo cuenta con una planilla con la siguiente información:
Se requiere un programa que permita totalizar la cantidad vendida de cada uno de los artículos que comercializa el kiosco imprimiendo un listado con el siguiente diseño:

Análisis
Para resolver este programa será necesario utilizar dos arrays de 100 posiciones cada uno. Un array para totalizar la cantidad vendida de cada artículo (arrCant) y otro array para totalizar los montos de facturados en cada ticket (arrMonto).
El problema se limita a leer los datos de la planilla y acumular los valores en los arrays, en la posición identificada por idArticulo. Recordemos que son 100 artículos numerados de 1 a 100.
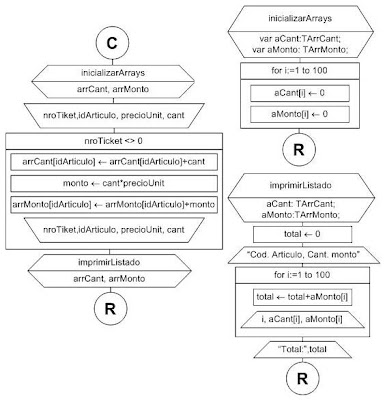
Ahora vamos a modificar el enunciado del problema anterior para ilustrar una situación muy común cuya resolución se facilita enormemente si disponemos de las funciones que analizamos más arriba.
Problema 5.4.1
Idem. problema 5.4 pero con las siguientes modificaciones:
1. idArticulo – valor alfanumérico, 3 caracteres.
2. El kiosco comercializa a lo sumo 100 artículos (pueden ser menos)
Análisis
Si bien puede no haber demasiada diferencia con el enunciado anterior, los cambios que se proponen en este problema complican bastante la resolución del ejercicio.
La principal diferencia es que el idArticulo ahora es alfanumérico y por este motivo no lo podemos utilizar como índice para acceder a los arrays.
Por otro lado, el kiosco no necesariamente comercializa 100 artículos diferentes. Podrían ser menos.
Para resolver este problema tendremos que explicar el concepto de array paralelo. Es decir: un array en el que iremos guardando los idArticulo. La posición que cada idArticulo ocupa en el array será la posición que utilizaremos para acceder a los otros arrays para acumular los montos y las cantidades.
Supongamos que la planilla tiene la siguiente información:
Entonces a medida que leemos cada idArticulo buscamosEInsertamos en un array (arrArticulo). La función nos retorna la posición donde se insertó o donde se encontró el idArticulo. Luego utilizamos esa posición para acumular en los otros arrays.
Vemos que tanto arrCant como arrMonto son arrays paralelos a arrArticulo. Es decir: por cada artículo que leamos de la planilla primero lo tendremos que buscar en arrArticulo para ver en que posición está y luego, con esa posición acceder a arrCant y a arrMonto para acumular las cantidades correspondientes.
Comparemos la solución del problema 5.4 con la solución del problema 5.4.1.
Comparando podemos notar la diferencia. En este caso, por cada idArticulo buscamos en el array arrArticulo en que posición está. Si aún no estaba entonces lo insertamos. La función buscarEInsertarOrdenado podría devolver un valor negativo (si es que el idArticulo no estaba y lo tuvo que insertar). Por ese motivo eliminamos el signo asignándole su valor absoluto.
Una vez que tenemos la posición en la que el idArticulo está ubicado en arrArticulo utilizamos esa posición para acceder a los otros array.
Podríamos decir que el acceso es indirecto. Primero accedemos al array paralelo para obtener la posición y luego, con esa posición accedemos a otros arrays. En cambio, en la solución de la derecha (del problema 5.4) el acceso es directo.
Ordenamiento
Hasta aquí trabajamos con arrays ordenados porque a medida que insertábamos los elementos lo hacíamos desplazando los mayores hacia abajo de forma tal que el array siempre mantenga su orden (con la función insertarOrdenado por ejemplo).
Veremos ahora un algoritmo que nos permitirá ordenar un array desordenados. El algoritmo burbuja.
La idea es la siguiente: recorrer el array de arriba (primer posición) a abajo (última posición) preguntando si el elemento de la posición [i] es mayor que el elemento de la posición [i+1]. Si se verifica esa pregunta entonces esos dos elementos están desordenados entre si. Así que se los permuta y se pregunta por el elemento en la posición [i+1] respecto del de la posición [i+2] y así sucesivamente.
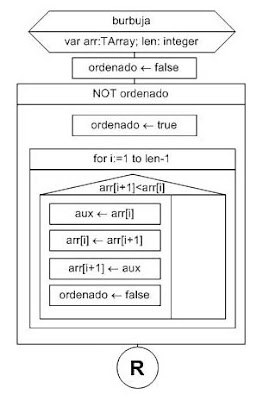
untArray.pas (implementación: procedure ordenar)
Búsqueda Binaria
Este algoritmo provee una búsqueda mucho más eficiente que la búsqueda secuencial. Parte de la supocición de que el array sobre el que se va a realizar la búsqueda está ordenado.
La idea es descartar "mitades" del array. Se hace un promedio (k) entre la primer posición (i) y la última (j) y se compara el elemento que se encuentra en esa posición promedio (arr[k]) respecto del valor que estamos buscando. Si coincide entonces el problema está resuelto. Si no coincide entonces el elemento encontrado podría ser mayor o menor. Si el elemento encontrado es menor quiere decir que el elemento que nosotros buscamos está en la segunda mitad. Si lo que encontramos es mayor entonces lo que buscamos está en la primer mitad del array.
Veamos un ejemplo: El array arr tiene 6 elementos y está ordenado. Buscamos el elemento 14.
Con i=1 y j=6 la posición promedio (haciendo k:=(i+j) div 2) es 3. Si el elemento que estamos buscando es el 14 entonces vemos que lo que encontramos (arr[k]=9) es menor que 14. Entonces descartamos la primer mitad asignando a i el valor de k+1.
En la imagen del medio vemos que i=4, j=6 y k=5. Buscamos el valor 14 y arr[k]=17. Entonces descartamos la segunda mitad haciendo j:=k-1 con lo que j queda en 4.
En la imagen de la derecha vemos que i=4, j=4 entonces k=4 y resulta que arr[4]=14. Encontramos lo que buscábamos.
¿Pero que pasa si buscamos un valor que no existe dentro del array? Busquemos el valor 8.
Vemos que los índices i y j terminan cruzados. Es decir: i resulta mayor que j. Esto nos indica que el valor que buscamos no existe en el array.
Ahora si, podemos ver el algoritmo.
La búsqueda binaria realiza un máximo de log2(len) comparaciones (siendo len la cantidad de elementos útiles del array).
untArray.pas (implementación: function buscarBin)
Matrices
Vimos que los arrays son conjuntos de variables del mismo tipo: arrays de integer, arrays de string, etc. ¿Que pasaría si definimos un array donde cada uno de sus elementos fuese un array? Un array de arrays...
Llamamos matriz a un array de arrays, y en Pascal se define así:
// notacion Pascal
var mat: array[1..3,1..4] of integer;
o bien así:
// notacion alternativa, tambien es valida
var mat: array[1..3] of array[1..4] of integer;
Problema 5.5
Leer los valores de una matriz numérica de 3 filas y 4 columnas. Primero los 4 valores de la fila 1, luego los de la fila 2 y luego los de la fila 3. Imprimir la matriz traspuesta.
Análisis
Primero analicemos una matriz de 3x4 con datos de ejemplo y estudiemos su traspuesta para entender lo que tiene que hacer el algoritmo.
La posibilidad de acceder a los elementos del array referenciándolos mediante un subíndice es fundamental y hace de los arrays un recurso indispensable para la resolución de cierto tipo de problemas.
Modifiquemos el programa testArray.pas para acceder automaticamente a las posiciones del array mediante el uso de ciclos for.
testArray2.pas
1:
2:var arr: array [1..5] of integer;
3: i: integer;
4:
5:begin
6: // cargo el array
7: for i:=1 to 5 do begin
8: arr[i]:= 2*i;
9: end;
10:
11: // muestro los elementos del array
12: for i:=1 to 5 do begin
13: writeln('valor del arr[',i,']=',arr[i]);
14: end;
15:end.
16:
Con el primer for cargamos el array. El for itera haciendo variar i entre 1 y 5. Por lo tanto en la primer iteración, cuando i vale 1 hablar de arr[i] es hablar de arr[1]. En la siguiente iteración i valdrá 2 entonces hablar de arr[i] es hablar de arr[2] y así.
Asignamos arr[i] := 2*i ya que (siguiendo con el ejemplo anterior) lo que queremos asignar en cada posición coincide con "el doble del índice" de cada posición del array.
Con el segundo for recorremos el array y mostramos lo que contiene en cada una de sus posiciones.
Es muy importante tener en cuenta que los arrays son estructuras de datos estáticas. Se definen antes de que comience a ejecutarse el algoritmo por lo tanto tenemos que definir de antemano su longitud (cantidad de elementos).
No podemos hacer esto:
var arr: array [1..n] of integer
Definir un array de (por ejemplo) 10 elementos no implica que (luego) necesariamente vayamos a utilizar esos 10 elementos. Podemos utilizar solo algunos o (a lo sumo) los 10. Obviamente, aunque solo utilicemos 1 de los 10 elementos del array la memoria reservada siempre será de 10 elementos durante toda la ejecución del programa.
Operaciones Sobre Arrays
Buscar, insertar, eliminar y ordenar elementos sobre un array son algunas de las operaciones que vamos a estudiar en este capítulo.
Analizaremos los siguientes procedimientos y funciones que definiremos en una unit.
untArray.pas
1:unit untArray;
2:
3:interface
4:
5:const
6: // podemos definir la longitud del array
7: // como una constante
8: LTArray = 10;
9:
10:type
11: // definimos un tipo de datos que represente
12: // a los arrays de este tipo:
13: // un array de 1 a LTArray (10) de integer
14: TArray = array [1..LTArray] of integer;
15:
16:// operaciones asociadas al manejo de arrays
17:
18:// inserta un elemento en el array, en una
19:// posicion especificada (pos) desplazando hacia
20:// abajo los elementos de las posiciones siguientes
21:procedure insertar(var arr: TArray
22: ; var len: integer
23: ; valor: integer
24: ; pos: integer);
25:
26:// elimina el elemento de la posicion especificada
27:// desplazando hacia arriba los elementos de las
28:// posiciones siguientes
29:procedure eliminar(var arr: TArray
30: ; var len: integer
31: ; pos: integer);
32:
33:// busca un elemento en el array y retorna la
34:// posicion donde lo encontro o un valor negativo
35:// si el elemento no se encontro en el array
36:function buscar(arr: TArray
37: ; len: integer
38: ; valor: integer): integer;
39:
40:// inserta un elemento en el array pero manteniendo
41:// el orden ascendente de los elementos, retorna la
42:// posicion en la que el elemento fue insertado
43:function insertarOrdenado(var arr: TArray
44: ; var len: integer
45: ; valor: integer): integer;
46:
47:// busca un elemento en el array. Si lo encuentra
48:// retorna su posicion, si no lo encuentra entonces
49:// lo inserta ordenado y retorna la posicion (en
50:// negativo) en la que el elemento fue insertado
51:function buscarEInsertarOrdenado(
52: var arr: TArray
53: ; var len: integer
54: ; valor: integer): integer;
55:
56:// busqueda binaria sobre el array (tema aparte)
57:function buscarBin(arr: TArray
58: ; len:integer
59: ; valor:integer): integer;
60:
61:// ordena los elementos del array (tema aparte)
62:procedure ordenar(var arr:TArray; len: integer);
63:
64:// la seccion implementation esta mas abajo
65:// :
66:
Notemos que todos los procedimientos y funciones reciben el parámetro len. Este parámetro indica la cantidad de elementos útiles del array. Es decir, si tenemos un array de 10 posiciones de las cuales hasta el momento ninguna está siendo utilizada entonces el valor del parámetro len será 0. Pero si en ese mismo array insertamos un valor entonces el parámetro len debe pasar a valer 1 ya que en el array ahora tenemos 1 elemento útil (y espacio libre para nueve elementos más que hasta el momento no están siendo utilizados).
procedure insertar (implementación)
El objetivo de este procedimiento es insertar un valor (valor) en una posición (pos) del array (arr) desplazando hacia abajo todos los elementos que se encuentran a partir de la posición pos inclusive.

En el gráfico vemos como queda el array luego de insertar el valor 5 en la posición 3. El valor que estaba en la posicion 4 pasó a la posición 5 y el valor que estaba en la posición 5 pasó a la posición 6.
Es importante notar como juega el valor del parámetro len. El parámetro len indica cuantas posiciones del array están siendo efectivamente utilizadas. En el primer caso el parámetro len vale 4 ya que el array contiene 4 elementos. El procedimiento insertar debe incrementar el valor del parámetro len para reflejar que (luego de insertar el nuevo elemento) el array tiene un elemento más.
Notemos que el array tiene una longitud de 10 elementos. Sin embargo no todos necesariamente tienen que ser utilizados. Justamente eso es lo que refleja el parámetro len. Los elementos útiles del array son los que están en las posiciones 1 a len.

Análisis
Utilizamos un for downto que comienza en len+1 y termina en pos+1.
Considerando el ejemplo anterior, tendremos: len=4 (entonces len+1=5) y pos=3 (o sea que pos+1=4). El for itera con i variando entre 5 y 4. En la primera vuelta (i vale 5) a arr[5] le asignamos arr[4]. En la próxima vuelta (i vale 4) a arr[4] le asignamos arr[3]. Luego asignamos valor a arr[pos].
Desplazamos todos los elementos hacia abajo para poder insertar el nuevo valor en la posición pos.
untArray.pas (implementación: procedure insertar)
1:
2:// comenzamos con la seccion implementation
3:implementation
4:
5:procedure insertar(var arr: TArray
6: ; var len: integer
7: ; valor: integer
8: ; pos: integer);
9:var i: integer;
10:begin
11: for i:=len+1 downto pos+1 do begin
12: arr[i]:= arr[i-1];
13: end;
14:
15: arr[pos]:=valor;
16: len:=len+1;
17:end;
18:
Con esto podemos resolver el siguiente problema.
Problema 5.1
Dado un conjunto de valores positivos (no serán más de 10 valores) imprimirlo en orden inverso. Fin de datos: valor negativo.

Análisis
Leemos valores mientras no se ingrese un valor negativo y los insertamos en el array arr, en la posición 1. Todos los insertamos en la primer posición.
Supongamos que los valores que ingresan son: { 3, 2, 1, -1 } entonces la secuencia será la siguiente.
Insertamos el 3 en la posicion 1. Luego insertamos el 2 en la posición 1 (desplazando el 3 a la posición 2). Luego insertamos el 1 en la posición 1 (desplazando el 2 a la posición 2 y el 3 a la posición 3). Así, al momento de recorrer e imprimir el array la salida será: 1, 2, 3.
Recordemos que el procedimiento insertar incrementa el valor del parámetro len cada vez que inserta un valor en el array.
problema5.1.pas
1:
2:uses untArray;
3:
4:var
5: arr: TArray;
6: i,n,len: integer;
7:
8:begin
9: len:=0;
10: readln(n);
11:
12: while( n>=0 ) do begin
13: insertar(arr,len,n,1);
14: readln(n);
15: end;
16:
17: for i:=1 to len do begin
18: writeln(arr[i]);
19: end;
20:end.
21:
procedure eliminar (implementación)
El objetivo de este procedimiento es eliminar el valor contenido en una posición del array desplazando una posición hacia arriba todos los elementos que se encuentren en las posiciones siguientes.
Análisis
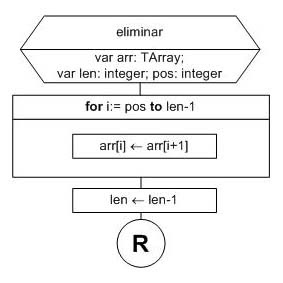
La solución para este algoritmo es simple. Asignar en la posición pos el elemento de la posición pos+1. Luego asignar en la posición pos+1 el elemento de la posición pos+2, y así, si hacemos variar a i entre pos y len-1 podemos asignar al array arr en la posición arr[i] el elemento de la posición arr[i+1].
Por último, la cantidad de elementos útiles del array decreció. Entonces tenemos que decrementar el valor del parámetro len (que recibimos por referencia).
untArray.pas (implementación: procedure eliminar)
1:
2:procedure eliminar(var arr: TArray
3: ; var len: integer
4: ; pos: integer);
5:var i: integer;
6:begin
7: for i:=pos to len-1 do begin
8: arr[i]:= arr[i+1];
9: end;
10: len:=len-1;
11:end;
12:
function buscar (implementación)
Este algoritmo lo implementamos como una función. El objetivo es buscar un elemento en el array. El elemento puede estar o no. Si el elemento está entonces la función retorna la posición en la cual se encontró el elemento. Si el elemento no está entonces la función retorna -1 para indicar que el elemento no se encontró en el array.
Análisis
Recorremos el array mientras no nos pasemos de la última posición (len) y mientras no encontremos el elemento que buscamos.
Cuando corta el while preguntamos por cual de las dos condiciones cortó. si cortó porque i es mayor que len entonces llegamos al final y no encontramos el elemento. Retornamos -1. Si cortó porque arr[i] = valor entonces lo encontró en la posición i. Retornamos el valor de i.
untArray.pas (implementación: function buscar)
1:
2:function buscar(arr: TArray
3: ; len: integer
4: ; valor: integer): integer;
5:var i:integer;
6:begin
7: i:=1;
8: while( (arr[i]<>valor) AND (i<=len) ) do begin
9: i:=i+1;
10: end;
11:
12: if( i>len ) then begin
13: buscar:= -1;
14: end else begin
15: buscar:= i;
16: end;
17:end;
18:
Problema 5.2
Leer un conjunto A de valores positivos (finaliza con un valor negativo). Luego leer otro conjunto B de valores positivos (finaliza con un valor negativo). Imprimir los valores del conjunto A que no pertenezcan al conjunto B. Se garantiza que los conjuntos no tendrán más de 10 valores.

Análisis
Leemos los valores del conjunto A y los insertamos en el array arr, en la posicion len+1 (es decir: siempre al final).
Luego leemos los valores del conjunto B y por cada valor buscamos en el array. Si se encuentra entonces lo eliminamos del array.
Por último, recorremos e imprimimos los elementos de arr que serán los elementos del conjunto A que no pertencen al conjunto B.
problema5.2.pas
1:
2:uses untArray;
3:
4:var
5: len,n,m,i,pos: integer;
6: arr: TArray;
7:begin
8: len:=0;
9:
10: // leemos el conjunto A y lo insertamos
11: // al final del array
12: write('Ingrese valores del conjunto A');
13: readln(n);
14: while( n>=0 ) do begin
15: insertar(arr,len,n,len+1);
16: read(n);
17: end;
18:
19: // leemos el conjunto B, buscamos y (si
20: // se encuentra) eliminamos el valor del array
21: write('Ingrese valores del conjunto B');
22: readln(m);
23: while( m>=0 ) do begin
24: pos:=buscar(arr,len,m);
25: if( pos>0 ) then begin
26: eliminar(arr,len,pos);
27: end;
28: read(m);
29: end;
30:
31: writeln('Resultado A-B:');
32: for i:=1 to len do begin
33: writeln(arr[i]);
34: end;
35:end.
36:
function insertarOrdenado (implementación)
El objetivo de esta función es insertar un elemento (valor) en el array (arr) pero considerando un orden de precedencia. Luego retorna la posición en la cual se insertó el elemento.
Análisis
Recorremos el array mientras no nos pasemos del último elemento útil (len) y mientras no encontremos un elemento mayor que el valor que nos piden insertar (valor). Cuando corta el while preguntamos por cual de las dos condiciones cortó. Si corto porque i es mayor que len entonces el array no contiene ningún elemento menor o igual que valor. Es el mayor y debemos insertarlo al final.
Si el while cortó porque arr[i] es mayor que valor entonces tenenos que insertar el elemento en la posición i. Llamamos al procedimiento insertar y retornamos el valor de i.
untArray.pas (implementación: function insertarOrdenado)
1:
2:function insertarOrdenado(var arr: TArray
3: ; var len: integer
4: ; valor: integer): integer;
5:var i:integer;
6:begin
7: i:=1;
8: while( (i<= len) AND (arr[i]<=valor) ) do begin
9: i:=i+1;
10: end;
11:
12: if( i>len ) then begin // inserto al final
13: len:=len+1;
14: arr[len]:=valor;
15: insertarOrdenado:=len;
16: end else begin // inserto en la posicion i
17: insertar(arr,len,valor,i);
18: insertarOrdenado:=i;
19: end;
20:end;
21:
function buscarEInsertarOrdenado (implementación)
Esta función es similar a la anterior. La diferencia es que antes de insertar el elemento verifica si ya existe en el array. Si ya existe entonces no lo inserta y devuelve la posición donde lo encontró. Si no existe entonces lo inserta respetando el orden de precedencia y retorna la posición donde lo insertó. Para indicar al usuario (quien llama a la función) si el elemento existía previamente o si lo tuvo que insertar, la función retorna su valor en positivo o en negativo. Es decir:
pos:= buscarEInsertarOrdenado(...);
- si pos es positivo entonces el elemento se encontró en la posición pos
- si pos es negativo entonces el elemento se insertó en la posición abs(pos)
A medida que vamos teniendo más funciones resueltas resulta más facil programar nuevas funciones.
Para resolver esta función primero buscamos el elemento valor. Si no lo encontramos entonces lo insertamos ordenado. En ret tenemos la posición donde se insertó el elemento pero la tenemos que negativizar para retornar ese mismo valor en negativo. De esta manera le indicamos al llamador (programa que invoca a esta función) que el elemento no estaba y entonces lo insertamos.
Si el elemento fue encontrado entonces simplemente retornamos la posición en la que se encontró.
untArray.pas (implementación: function buscarEInsertarOrdenado)
1:
2:function buscarEInsertarOrdenado(
3: var arr: TArray
4: ; var len: integer
5: ; valor: integer): integer;
6:var i, ret: integer;
7:begin
8: i:=buscar(arr,len,valor);
9: if( i<0 ) then begin
10: ret:=insertarOrdenado(arr,len,valor);
11:
12: // negativizamos el valor de ret
13: ret:= 0-ret;
14: end else begin
15: ret:=i;
16: end;
17: buscarEInsertarOrdenado:=ret;
18:end;
19:
Problema 5.3
Leer un conjunto de valores e imprimirlos ordenados, sin repetición. El conjunto finaliza con un valor cero. No tendrá más de 10 valores. Indicar cuantos valores repetidos tiene el conjunto.

Análisis
El problema es muy simple. Leemos los valores del conjunto mientras no se ingrese el elemento final identificado por un valor cero. Tenemos un array arr en el cual buscamosEInsertamos los valores del conjunto. Es decir: solo insertamos si no existen previamente. Los que se repiten los podemos identificar porque la función buscarEInsertarOrdenado los encontrará en el array y retornará un valor positivo entonces en contRep contamos la cantidad de valores repetidos del conjunto. Al finalizar el ingreso de datos, el array contendrá todos los elementos no repetidos del conjunto y estos estarán ordenados.
problema 5.3.pas
1:
2:uses untArray;
3:
4:var
5: contRep, len,i, v,pos: integer;
6: arr:TArray;
7:begin
8: contRep:=0;
9: len:=0;
10: readln(v);
11:
12: while( v <> 0 ) do begin
13: pos:=buscarEInsertarOrdenado(arr,len,v);
14: if( pos>0 ) then begin
15: contRep:=contrep+1;
16: end;
17:
18: readln(v);
19: end;
20:
21: writeln('Repetidos: ',contRep);
22: for i:=1 to len do begin
23: writeln(arr[i]);
24: end;
25:end.
26:
Problema 5.4
Un kiosco vende 100 artículos diferentes. Al finalizar el día de trabajo cuenta con una planilla con la siguiente información:
- nroTicket
- idArticulo [1..100]
- cantidad
- precioUnit
Se requiere un programa que permita totalizar la cantidad vendida de cada uno de los artículos que comercializa el kiosco imprimiendo un listado con el siguiente diseño:

Análisis
Para resolver este programa será necesario utilizar dos arrays de 100 posiciones cada uno. Un array para totalizar la cantidad vendida de cada artículo (arrCant) y otro array para totalizar los montos de facturados en cada ticket (arrMonto).
El problema se limita a leer los datos de la planilla y acumular los valores en los arrays, en la posición identificada por idArticulo. Recordemos que son 100 artículos numerados de 1 a 100.

Ahora vamos a modificar el enunciado del problema anterior para ilustrar una situación muy común cuya resolución se facilita enormemente si disponemos de las funciones que analizamos más arriba.
Problema 5.4.1
Idem. problema 5.4 pero con las siguientes modificaciones:
1. idArticulo – valor alfanumérico, 3 caracteres.
2. El kiosco comercializa a lo sumo 100 artículos (pueden ser menos)
Análisis
Si bien puede no haber demasiada diferencia con el enunciado anterior, los cambios que se proponen en este problema complican bastante la resolución del ejercicio.
La principal diferencia es que el idArticulo ahora es alfanumérico y por este motivo no lo podemos utilizar como índice para acceder a los arrays.
Por otro lado, el kiosco no necesariamente comercializa 100 artículos diferentes. Podrían ser menos.
Para resolver este problema tendremos que explicar el concepto de array paralelo. Es decir: un array en el que iremos guardando los idArticulo. La posición que cada idArticulo ocupa en el array será la posición que utilizaremos para acceder a los otros arrays para acumular los montos y las cantidades.
Supongamos que la planilla tiene la siguiente información:
Entonces a medida que leemos cada idArticulo buscamosEInsertamos en un array (arrArticulo). La función nos retorna la posición donde se insertó o donde se encontró el idArticulo. Luego utilizamos esa posición para acumular en los otros arrays.
Vemos que tanto arrCant como arrMonto son arrays paralelos a arrArticulo. Es decir: por cada artículo que leamos de la planilla primero lo tendremos que buscar en arrArticulo para ver en que posición está y luego, con esa posición acceder a arrCant y a arrMonto para acumular las cantidades correspondientes.
Comparemos la solución del problema 5.4 con la solución del problema 5.4.1.
.Problema 5.4.......................Problema 5.4.1
Comparando podemos notar la diferencia. En este caso, por cada idArticulo buscamos en el array arrArticulo en que posición está. Si aún no estaba entonces lo insertamos. La función buscarEInsertarOrdenado podría devolver un valor negativo (si es que el idArticulo no estaba y lo tuvo que insertar). Por ese motivo eliminamos el signo asignándole su valor absoluto.
Una vez que tenemos la posición en la que el idArticulo está ubicado en arrArticulo utilizamos esa posición para acceder a los otros array.
Podríamos decir que el acceso es indirecto. Primero accedemos al array paralelo para obtener la posición y luego, con esa posición accedemos a otros arrays. En cambio, en la solución de la derecha (del problema 5.4) el acceso es directo.
Ordenamiento
Hasta aquí trabajamos con arrays ordenados porque a medida que insertábamos los elementos lo hacíamos desplazando los mayores hacia abajo de forma tal que el array siempre mantenga su orden (con la función insertarOrdenado por ejemplo).
Veremos ahora un algoritmo que nos permitirá ordenar un array desordenados. El algoritmo burbuja.
La idea es la siguiente: recorrer el array de arriba (primer posición) a abajo (última posición) preguntando si el elemento de la posición [i] es mayor que el elemento de la posición [i+1]. Si se verifica esa pregunta entonces esos dos elementos están desordenados entre si. Así que se los permuta y se pregunta por el elemento en la posición [i+1] respecto del de la posición [i+2] y así sucesivamente.

Análisis
El algoritmo itera el array desde 1 hasta len-1 y compara cada posición respecto de la siguiente. Si la posición arr[i+1] es menor que arr[i] entonces esos elementos están desordenados entre sí y los permuta. Luego compara arr[i+2] respecto de arr[i+1] y así hasta comparar arr[len] respecto de arr[len-1].
Luego de terminar la iteración del array (es decir, luego de que termina el ciclo for) el array queda un poco más ordenado. Es decir que forzando una nueva recorrida lo podremos ordenar un poco más. Para esto se utiliza la variable ordenado. Esta variable comienza en false pero ni bien ingresamos al while se pone en true. Si realizamos al menos una permutación la ponemos en false para forzar una nueva iteración del while y así una nueva barrida del array.
Pongamos el siguiente ejemplo. Un array arr = { 4, 3, 2, 1 } en ese orden. Está desordenado si consideramos un orden ascendente. El len (elementos útiles) del array será 4.
En la figura de la izquierda vemos la primer iteración del ciclo while (es decir: las primeras 4 iteraciones del ciclo for)
Vemos que para un array de 4 elementos totalmente desordenados, en la primer pasada del for se realizarán 3 permutaciones.
En la figura de la derecha vemos la segunda iteración del while (próximas 4 iteraciones del for). Podemos ver que en este caso solo se realizan 2 iteraciones ya que el array está un poco más ordenado que al principio.
Veamos las próximas iteraciones del while.
En la tercer iteración del while (figura de la izquierda), dentro del for solo se realiza una única permutación. Si bien el array queda ordenado, la variable ordenado quedó en false con lo cual se fuerza una nueva iteración del while (figura de la derecha). En esta última iteración, dentro del for no se realiza ninguna permutación. Así que la variable ordenado permanecerá en true y así finaliza el algoritmo.
El algoritmo itera el array desde 1 hasta len-1 y compara cada posición respecto de la siguiente. Si la posición arr[i+1] es menor que arr[i] entonces esos elementos están desordenados entre sí y los permuta. Luego compara arr[i+2] respecto de arr[i+1] y así hasta comparar arr[len] respecto de arr[len-1].
Luego de terminar la iteración del array (es decir, luego de que termina el ciclo for) el array queda un poco más ordenado. Es decir que forzando una nueva recorrida lo podremos ordenar un poco más. Para esto se utiliza la variable ordenado. Esta variable comienza en false pero ni bien ingresamos al while se pone en true. Si realizamos al menos una permutación la ponemos en false para forzar una nueva iteración del while y así una nueva barrida del array.
Pongamos el siguiente ejemplo. Un array arr = { 4, 3, 2, 1 } en ese orden. Está desordenado si consideramos un orden ascendente. El len (elementos útiles) del array será 4.
En la figura de la izquierda vemos la primer iteración del ciclo while (es decir: las primeras 4 iteraciones del ciclo for)
Vemos que para un array de 4 elementos totalmente desordenados, en la primer pasada del for se realizarán 3 permutaciones.
En la figura de la derecha vemos la segunda iteración del while (próximas 4 iteraciones del for). Podemos ver que en este caso solo se realizan 2 iteraciones ya que el array está un poco más ordenado que al principio.
Veamos las próximas iteraciones del while.
En la tercer iteración del while (figura de la izquierda), dentro del for solo se realiza una única permutación. Si bien el array queda ordenado, la variable ordenado quedó en false con lo cual se fuerza una nueva iteración del while (figura de la derecha). En esta última iteración, dentro del for no se realiza ninguna permutación. Así que la variable ordenado permanecerá en true y así finaliza el algoritmo.
1:
2:procedure ordenar(var arr:TArray; len: integer);
3:var ordenado: boolean; i,aux: integer;
4:begin
5: ordenado:= false;
6: while( NOT ordenado ) do begin
7: ordenado:=true;
8: for i:=1 to len-1 do begin
9: if( arr[i+1]<arr[i] ) then begin
10: aux:=arr[i];
11: arr[i]:=arr[i+1];
12: arr[i+1]:=aux;
13: ordenado:=false;
14: end;
15:
16: end;
17: end;
18:end;
19:
Búsqueda Binaria
Este algoritmo provee una búsqueda mucho más eficiente que la búsqueda secuencial. Parte de la supocición de que el array sobre el que se va a realizar la búsqueda está ordenado.
La idea es descartar "mitades" del array. Se hace un promedio (k) entre la primer posición (i) y la última (j) y se compara el elemento que se encuentra en esa posición promedio (arr[k]) respecto del valor que estamos buscando. Si coincide entonces el problema está resuelto. Si no coincide entonces el elemento encontrado podría ser mayor o menor. Si el elemento encontrado es menor quiere decir que el elemento que nosotros buscamos está en la segunda mitad. Si lo que encontramos es mayor entonces lo que buscamos está en la primer mitad del array.
Veamos un ejemplo: El array arr tiene 6 elementos y está ordenado. Buscamos el elemento 14.
Con i=1 y j=6 la posición promedio (haciendo k:=(i+j) div 2) es 3. Si el elemento que estamos buscando es el 14 entonces vemos que lo que encontramos (arr[k]=9) es menor que 14. Entonces descartamos la primer mitad asignando a i el valor de k+1.
En la imagen del medio vemos que i=4, j=6 y k=5. Buscamos el valor 14 y arr[k]=17. Entonces descartamos la segunda mitad haciendo j:=k-1 con lo que j queda en 4.
En la imagen de la derecha vemos que i=4, j=4 entonces k=4 y resulta que arr[4]=14. Encontramos lo que buscábamos.
¿Pero que pasa si buscamos un valor que no existe dentro del array? Busquemos el valor 8.
Vemos que los índices i y j terminan cruzados. Es decir: i resulta mayor que j. Esto nos indica que el valor que buscamos no existe en el array.
Ahora si, podemos ver el algoritmo.
La búsqueda binaria realiza un máximo de log2(len) comparaciones (siendo len la cantidad de elementos útiles del array).
untArray.pas (implementación: function buscarBin)
1:
2:function buscarBin(arr: TArray
3: ; len:integer
4: ; valor:integer): integer;
5:var i,j,k: integer; encontrado: boolean;
6:begin
7: encontrado:=false;
8: i:=0;
9: j:=len;
10:
11: while( (i<=j) AND (NOT encontrado) ) do begin
12: k:= (i+j) div 2;
13: if( arr[k] = valor ) then begin
14: encontrado:=true;
15: end else begin
16: if( arr[k]< valor ) then begin
17: i:=k+1;
18: end else begin
19: j:=k-1;
20: end;
21: end;
22: end;
23:
24: if( i>j ) then begin
25: buscarBin:=-1;
26: end else begin
27: buscarBin:=k;
28: end;
29:end;
30:
31:end. // fin untArray.pas
32:
Matrices
Vimos que los arrays son conjuntos de variables del mismo tipo: arrays de integer, arrays de string, etc. ¿Que pasaría si definimos un array donde cada uno de sus elementos fuese un array? Un array de arrays...
Llamamos matriz a un array de arrays, y en Pascal se define así:
// notacion Pascal
var mat: array[1..3,1..4] of integer;
o bien así:
// notacion alternativa, tambien es valida
var mat: array[1..3] of array[1..4] of integer;
Problema 5.5
Leer los valores de una matriz numérica de 3 filas y 4 columnas. Primero los 4 valores de la fila 1, luego los de la fila 2 y luego los de la fila 3. Imprimir la matriz traspuesta.
Análisis
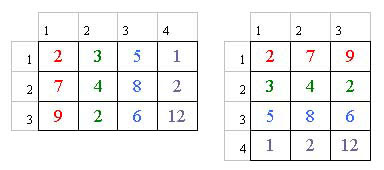
Primero analicemos una matriz de 3x4 con datos de ejemplo y estudiemos su traspuesta para entender lo que tiene que hacer el algoritmo.

Vemos que si la matriz original es de 3x4 entonces su traspuesta es de 4x3, de forma tal que las columnas de la matriz original pasan a ser las filas de la matriz traspuesta.
Entonces el algoritmo consiste en leer los valores, cargarlos en una matriz y luego recorrer la matriz por columnas.
Entonces el algoritmo consiste en leer los valores, cargarlos en una matriz y luego recorrer la matriz por columnas.

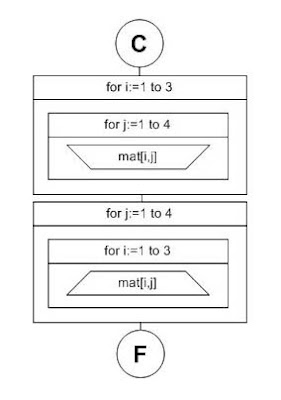
Como vemos manejamos 2 pares de ciclos for anidados. El primero es para leer los valores de la matriz. La variable i representa las filas y la variable j representa las columnas. Entonces si i varía entre 1 y 3 y por cada valor de i, j varía entre 1 y 4, cuando leemos en mat[i,j] estamos leyendo cada una de las celdas de la matriz, comenzando de arriba hacia abajo (filas) y de izquierda a derecha (columnas).
El segundo par de ciclos for anidados es para imprimir los valores. Notemos que en este caso el for externo hace variar j entre 1 y 4 y el interno hace que i varíe entre 1 y 3. Con esto recorremos la matriz por columnas y así logramos imprimir la matriz traspuesta.
problema5.5.pas
Arrays Multidimensionales
Así como una matriz es un "array de arrays", si consideramos una "matriz de arrays" tendremos un array de 3 dimensiones: un "array de arrays de arrays" o simplemente un array 3d.
// notacion
var x: array[1..3,1..4,1..4] of iteger;
Luego de la definición anterior x será un array de 3 dimensiones y lo podemos representar así:
La primer dimensión representa las filas, la segunda representa las columnas y la tercer dimensión representa la profundidad (o plano).
.
Algoritmos y Estructuras de Datos UTN - UBA.
El segundo par de ciclos for anidados es para imprimir los valores. Notemos que en este caso el for externo hace variar j entre 1 y 4 y el interno hace que i varíe entre 1 y 3. Con esto recorremos la matriz por columnas y así logramos imprimir la matriz traspuesta.
problema5.5.pas
1:
2:var
3: mat: array [1..3,1..4] of integer;
4: i,j: integer;
5:begin
6: // recorro las filas
7: for i:=1 to 3 do begin
8: write('Ingrese fila ',i,' :');
9:
10: // recorro las columnas
11: for j:=1 to 4 do begin
12: readln(mat[i,j]);
13: end;
14: end;
15:
16: // recorro las columnas
17: for j:=1 to 4 do begin
18: // recorro las filas
19: for i:=1 to 3 do begin
20: write( mat[i][j],' ' );
21: end;
22: writeln();
23: end;
24:end.
25:
Arrays Multidimensionales
Así como una matriz es un "array de arrays", si consideramos una "matriz de arrays" tendremos un array de 3 dimensiones: un "array de arrays de arrays" o simplemente un array 3d.
// notacion
var x: array[1..3,1..4,1..4] of iteger;
Luego de la definición anterior x será un array de 3 dimensiones y lo podemos representar así:
La primer dimensión representa las filas, la segunda representa las columnas y la tercer dimensión representa la profundidad (o plano).
.
Algoritmos y Estructuras de Datos UTN - UBA.

















3 comentarios:
En los diagramas utilizas el elemento utilizado para graficar los WHILE en los FOR, los esquemas son distintos.
cometiste un error, en la resolucion del problema 5.3, porqe vos estas contando CADA vez q se repite un numero, pero NO cuantos numeros distintos se repiten. Es una peqeña diferencia, pero es;)
Es un tema de interpretación del enunciado. La resolución está bien.
Saludos,
Pablo.
Publicar un comentario