.
Procedimientos y Funciones
El uso de procedimientos y funciones tiene dos objetivos bien definidos:
- La reutilización de código (o de algoritmos).
- La modularización de un algoritmo complejo en partes más simples, pequeñas y fáciles de resolver.
Justamente eso es lo que permiten hacer las funciones.
Funciones
Una función es un subprograma que al al ser invocado retorna un valor en función de los argumentos que recibe. Igual que las funciones matemáticas.
Por ejemplo la función seno(x)
si x vale 90 entonces seno(x) = 1
si x vale 0 entonces seno(x) = 0
si x vale 270 entonces seno(x) = -1
Vemos que el resultado de la función seno(x) depende del valor del argumento x. De la misma manera podemos definir funciones para luego invocarlas desde nuestros programas.
Volveremos a analizar el problema de mostrar el factorial del número ingresado pero considerando ahora la función factorial.
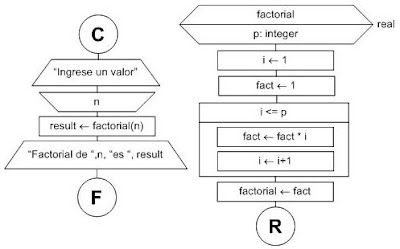
Análisis
A la izquierda vemos el programa principal. Leemos el valor e invocamos a la función factorial pasándole como parámetro el valor leido (n). El resultado lo almacenamos en la variable result y luego lo mostramos.
A la derecha vemos el diagrama de la función factorial. Esta función recibe un parámetro (p), calcula su factorial y retorna ese valor.
Recordemos que Pascal es un lenguaje fuertemente tipado por lo tanto tenemos que especificar el tipo de datos de los parámetros y del valor de retorno de la función.
En el caso de la función factorial hemos especificado que el parámetro p será de tipo integer y el valor de retorno de la función sera de tipo real (esto lo estudiaremos más adelante).
Por último, el valor que queremos retornar al momento de invocar la función debe ser asignado al mismo nombre de la función (como si el nombre de la función fuera una variable).
testFuncionFactorial.pas
Reusabilidad del Código
Es obvio que ya que programamos la función factorial que nos permite calcular el factorial de un número especificado vamos a querer utilizarla siempre que tengamos un número para el cual necesitemos calcular su factorial.
Es decir que siempre que identifiquemos funciones independientes sería bueno poderlas tener por separado, de forma tal que vayamos conformando nuestra propia librería de funciones para poderlas invocar desde cualquier programa donde las necesitemos.
En Pascal podemos tener archivos que solo contengan funciones y procedimientos para luego invocarlos desde nuestros programas. Estos archivos son llamados unidades (o unit). A continuación veremos una unit en el que definiremos la función factorial.
libreria.pas
Cuando hablamos de prototipo de la función nos referimos al encabezado. Esto es: nombre de la función, parámetros, tipos de los parámetros y tipo del valor de retorno. El prototipo de la función factorial es el siguiente:
Este prototipo indica que se trata de una función llamada factorial, que recibe un parámetro de tipo integer y retorna un valor de tipo real.
Luego el programa principal que invoca a la función factorial será:
testLiberia.pas
Notemos que para poder acceder a las funciones y procedimientos definidos en la unit libreria debemos indicar la sententencia: uses libreria.
Procedimientos
Al igual que las funciones, los procedimientos son subprogramas. La diferencia es que los procedimientos no tienen valor de retorno. La única forma de devolver algún valor que tiene un procedimiento es modificando el valor de los parámetros. Para esto el parámetros deben recibirse por referencia.
Parámetros por valor y por referencia
Los parámetros se pueden recibir por valor o por referencia. Cuando se reciben por valor, el procedimiento o la función no puede modificar su valor. Cuando se reciben por referencia el procedimiento o la función puede modificarlo.
El ejemplo típico para analizar esto es un procedimiento permutar(a,b). Recibe dos parámetros y permuta sus valores.
Analicemos el siguiente problema para estudiar este caso.
Problema 3.1
Leer dos valores numéricos por teclado. Realizar un procedimiento que los reciba y los permute.
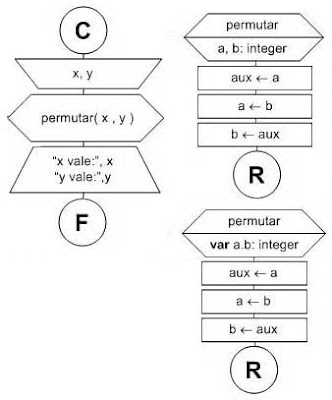
Análisis
El programa principal simplemente lee los valores x e y, e invoca al procedimiento permutar pasándole como parámetro los dos valores. Luego muestra el valor de x y el valor de y.
Diagramamos dos versiones del procedimiento permutar. Las dos versiones son idénticas. La única diferencia está en la definición de los parámetros (en la versión de abajo se antepone la palabra var).
Cuando un procedimiento o una función recibe parámetros anteponiendo la palabra var los parámetros se reciben por referencia con lo cual su valor podrá ser modificado dentro del procedimiento. En cambio, si no se antepone la palabra var los parámetros se reciben por valor, lo que significa que si se los modifica dentro del procedimiento o función la modificación solo será válida dentro de ese contexto (dentro del procedimiento) pero al salir de este (y retornar al programa principal) sus valores originales no se verán modificados.
Probemos esto en Pascal.
problema3.1.pas
Si compilamos y ejecutamos este programa veremos que el procedimiento permutar efectivamente permuta los valores de los parámetros x e y.
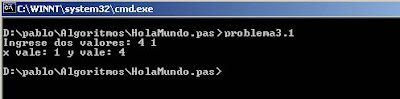
Ingresamos los valores x=4 e y=1 pero el programa al mostrar los valores de x e y muestra 1 y 4. El procedimiento permutar permutó sus valores.
Una prueba interesante para el lector será eliminar el prefijo var de los parámetros del procedimiento permutar y volver a ejecutar el programa. Podrá observar que los valores no se modifican.
Tipos de Datos
Cuando definimos variables e indicamos que son de un tipo de datos en particular estamos indicando la cantidad de bytes de memoria que se reservará para almacenar los valores que estas variables puedan contener durante la corrida del programa.
Como la cantidad de bytes definida para cada tipo de datos es una cantidad finita resulta que los valores que las variables vayan a contener estarán acotados por estas cantidades finitas de bytes.
Por ejemplo:
El tipo integer implica 2 bytes con bit de signo. Veamos la representación de estos bytes.
Vemos que de los 16 bits que componen los 2 bytes del integer solo se utilizan 15 ya que el más significativo (el primero comenzando desde la izquierda) es el bit de signo. 0 indica que el número representado en estos dos bytes es positivo y 1 indica que el número representado es negativo.
El mayor número que podemos almacenar en una variable de 2 bytes con signo (o sea un integer) es el número binario:
Cada bit del número binario representa una potencia de 2. El menos significativo (el más a la derecha) representa la potencia 0 (es decir 2 elevado a la cero) que vale 1. El siguiente (hacia la izquierda) representa la potencia 1 (o sea 2 elevado a la 1) que vale 2 y así.
La conversión entonces surje de sumar los valores representados por los bits del número binario que estén en 1.
b1 = |00000000|00010000| en decimal es 16 ya que solo sumamos el valor representado por el bit que está en 1.
b2 = |00000000|00010001| en decimal es 17. Resulta de sumar los valores representados por los bits en las posiciones 0 y 4, es decir: 2 elevado a la cero + 2 elevado a la 4. Resulta: 1+16 = 17.
Vemos entonces que el mayor número que podemos obtener en 2 bytes con bit de signo (es decir ignorando el bit más a la izquierda) es el número representado por todos unos salvo el de signo.
Luego sumamos las potencias de 2 representadas por todos esos unos (2 a la cero + 2 a la 1 + ...+ 2 a la 15). Esto da: 32767. Este es el mayor número que puede contener una variable de tipo integer. Y el menor será un número binario con todos los bits en 1, incluso el de signo. Estó es -32768.
En reglas generales diremos que en n bits, el mayor número entero decimal que podemos almacenar es (2 a la n) -1.
En Pascal podemos utilizar los siguientes tipos de datos:
Numéricos Enteros:
Numéricos Reales
Alfanuméricos
Problema 3.2
Considere dos circunferencias en un plano y un conjunto de 10 puntos. Realizar un programa que indique:
Análisis
Veamos un gráfico para poder comprender mejor el problema.
Consideremos la circunferencia 1. Dado un punto (xp, yp) podemos calcular la distancia entre este punto y el punto central de la circunferencia (x1, y1). Luego, si esa distancia es mayor que el radio, el punto estará afuera de la circunferencia. Si la distancia es menor o igual que el radio, el punto estará adentro de la circunferencia. Si la distancia es igual a cero el punto estará en el centro.
Por lo tanto los puntos en cuestión son: (x1, y1) y (xp, yp). La distancia entre esos puntos se puede calcular como:
El problema entonces consiste en leer los 10 puntos, por cada punto calcular la distancia al centro de cada una de las circunferencias y mantener los contadores que correspondan.
Para resolver el problema definimos la funcion procesaCirc. Esta función recibe los datos de una circunferencia (r, x1, y1), los datos de un punto (xp,yp) y retorna un valor negativo o positivo según el punto esté dentro o fuera de la circunferencia.
Además, la función se encarga de incrementar los contadores que correspondan. Por este motivo también recibe el contador de puntos dentro (cCirc1 o cCirc2) el contador de puntos fuera (cFue1 o cFue2) y el contador de puntos en el centro (cCentro1 o cCentro2). Como estos contadores serán incrementados dentro de la función (según corresponda) deben recibirse por referencia (anteponiendo la palabra var) para que la función pueda modificar su valor.
Analizando la función vemos que calcula la distancia (d) entre los dos puntos (cx,cy) y (px,py), y luego evalúa: si d<=r (radio) entonces el punto está dentro de la circunferencia por lo tanto incrementa cDentro. Luego pregunta si d=0 para incrementar cCentro. Si el punto no está adentro entonces estará afuera así que incrementa cFuera.
El valor de retorno de la función debe ser un valor negativo si el punto está adentro o un valor positivo si el punto está afuera de la circunferencia. La diferencia entre la distancia (d) y el radio (r) (negativa si la distancia es menor que el radio y positiva si la distancia es mayor) es el valor de retorno que necesitamos devolver en la función.
Ahora, analizando el programa principal: leemos los 10 puntos (xp, yp) y por cada punto invocamos dos veces a la función procesaCirc. La invocamos con los datos de la circunferencia 1 (r1, x1, y1) y luego la invocamos con los datos de la circunferencia 2 (r2, x2, y2) . Si ambos resultados son negativos entonces el punto está dentro de las dos circunferencias: está en la intersección así que incrementamos cInter. En cambio, si los dos resultados fueron positivos entonces el punto no está dentro de ninguna de las dos circunferencias. Incrementamos cNing.
problema3.2.pas
Argumentos en Línea de Comandos
Muchas veces necesitamos pasarle parámetros (o argumentos) directamente al programa principal. Ejemplos de esto son:
En Pascal (y en todos los lenguajes de programación) podemos hacer que nuestros programas reciban este tipo de argumentos. Veamos el siguiente ejemplo.
testArg1.pas
Este programa recibe argumentos en línea de comandos, muestra la cantidad de argumentos que recibe y luego muestra cada uno de esos argumentos.
Pascal provee las funciones paramCount y paramStr. La primera retorna la cantidad de parámetros que el programa está recibiendo (ver línea 6). Si no recibió ningún parámetro entonces retorna cero. La segunda recibe el número del parámetro al cual queremos acceder y retorna el parámetro ubicado en dicha posición. Es decir: si queremos leer el valor del primer parámetro le pasamos 1, si queremos leer el valor del segundo parámetro le pasamos 2 y así sucesivamente (ver línea 15).
Luego de compilar este programa podemos ejecutarlo y pasarle parámetros como vemos a continuación.
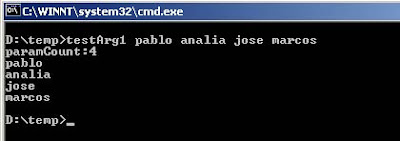
En la imagen vemos que se invoca al programa testArg1 con los parámetros pablo, analia, jose y marcos. El programa muestra la cantidad de parámetros recibidos (4) y luego muestra cada uno de estos parámetros, uno debajo del otro.
Algoritmos y Estructuras de Datos UTN - UBA..
A la derecha vemos el diagrama de la función factorial. Esta función recibe un parámetro (p), calcula su factorial y retorna ese valor.
Recordemos que Pascal es un lenguaje fuertemente tipado por lo tanto tenemos que especificar el tipo de datos de los parámetros y del valor de retorno de la función.
En el caso de la función factorial hemos especificado que el parámetro p será de tipo integer y el valor de retorno de la función sera de tipo real (esto lo estudiaremos más adelante).
Por último, el valor que queremos retornar al momento de invocar la función debe ser asignado al mismo nombre de la función (como si el nombre de la función fuera una variable).
testFuncionFactorial.pas
1:
2:// funcion factorial
3:function factorial(p:integer):real;
4:var i:integer; fact:real;
5:begin
6: i:=1;
7: fact:=1;
8: while( i<=p ) do begin
9: fact := fact*i;
10: i:=i+1;
11: end;
12:
13: factorial:=fact;
14:end;
15:
16:// programa principal
17:var n:integer; result:real;
18:begin
19: write('Ingrese un valor: ');
20: readln(n);
21: result:=factorial(n);
22: writeln('Resultado: ',result);
23:end.
24:
Reusabilidad del Código
Es obvio que ya que programamos la función factorial que nos permite calcular el factorial de un número especificado vamos a querer utilizarla siempre que tengamos un número para el cual necesitemos calcular su factorial.
Es decir que siempre que identifiquemos funciones independientes sería bueno poderlas tener por separado, de forma tal que vayamos conformando nuestra propia librería de funciones para poderlas invocar desde cualquier programa donde las necesitemos.
En Pascal podemos tener archivos que solo contengan funciones y procedimientos para luego invocarlos desde nuestros programas. Estos archivos son llamados unidades (o unit). A continuación veremos una unit en el que definiremos la función factorial.
libreria.pas
1:
2:// nombre de la unit (debe coincidar con el nombre
3:// del archivo)
4:unit libreria;
5:
6:interface
7:// en esta seccion se definen los prototipos de los
8:// procedimientos y funciones que tendremos en
9:// este archivo
10:
11: function factorial(p:integer):real;
12:
13:implementation
14:// en esta seccion se programan los prodecimientos
15:// y funciones definidos en la seccion interface
16:
17:function factorial(p:integer):real;
18:var i:integer; fact:real;
19:begin
20: i:=1;
21: fact:=1;
22: while( i<=p ) do begin
23: fact := fact*i;
24: i:=i+1;
25: end;
26:
27: factorial:=fact;
28:end;
29:
30:// las unit deben terminar con un "end."
31:end.
32:
Cuando hablamos de prototipo de la función nos referimos al encabezado. Esto es: nombre de la función, parámetros, tipos de los parámetros y tipo del valor de retorno. El prototipo de la función factorial es el siguiente:
function factorial(p: integer): real
Este prototipo indica que se trata de una función llamada factorial, que recibe un parámetro de tipo integer y retorna un valor de tipo real.
Luego el programa principal que invoca a la función factorial será:
testLiberia.pas
1:
2:// indico que voy a usar funciones definidas
3:// en una unit llamada "libreria"
4:uses libreria;
5:
6:var n:integer; result:real;
7:begin
8: write('Ingrese un valor: ');
9: readln(n);
10: result:=factorial(n);
11: writeln('Resultado: ',result);
12:end.
13:
Notemos que para poder acceder a las funciones y procedimientos definidos en la unit libreria debemos indicar la sententencia: uses libreria.
Procedimientos
Al igual que las funciones, los procedimientos son subprogramas. La diferencia es que los procedimientos no tienen valor de retorno. La única forma de devolver algún valor que tiene un procedimiento es modificando el valor de los parámetros. Para esto el parámetros deben recibirse por referencia.
Parámetros por valor y por referencia
Los parámetros se pueden recibir por valor o por referencia. Cuando se reciben por valor, el procedimiento o la función no puede modificar su valor. Cuando se reciben por referencia el procedimiento o la función puede modificarlo.
El ejemplo típico para analizar esto es un procedimiento permutar(a,b). Recibe dos parámetros y permuta sus valores.
Analicemos el siguiente problema para estudiar este caso.
Problema 3.1
Leer dos valores numéricos por teclado. Realizar un procedimiento que los reciba y los permute.

Análisis
El programa principal simplemente lee los valores x e y, e invoca al procedimiento permutar pasándole como parámetro los dos valores. Luego muestra el valor de x y el valor de y.
Diagramamos dos versiones del procedimiento permutar. Las dos versiones son idénticas. La única diferencia está en la definición de los parámetros (en la versión de abajo se antepone la palabra var).
Cuando un procedimiento o una función recibe parámetros anteponiendo la palabra var los parámetros se reciben por referencia con lo cual su valor podrá ser modificado dentro del procedimiento. En cambio, si no se antepone la palabra var los parámetros se reciben por valor, lo que significa que si se los modifica dentro del procedimiento o función la modificación solo será válida dentro de ese contexto (dentro del procedimiento) pero al salir de este (y retornar al programa principal) sus valores originales no se verán modificados.
Probemos esto en Pascal.
problema3.1.pas
1:
2:// recibe dos parametros y permuta sus valores
3:procedure permutar(var a,b: integer);
4:var aux: integer;
5:begin
6: aux:= a;
7: a:= b;
8: b:= aux;
9:end;
10:
11:// programa principal
12:var x,y: integer;
13:begin
14: write('Ingrese dos valores: ');
15: readln(x,y);
16: permutar(x,y);
17: writeln('x vale: ',x,' y vale: ',y);
18:end.
19:
Si compilamos y ejecutamos este programa veremos que el procedimiento permutar efectivamente permuta los valores de los parámetros x e y.

Ingresamos los valores x=4 e y=1 pero el programa al mostrar los valores de x e y muestra 1 y 4. El procedimiento permutar permutó sus valores.
Una prueba interesante para el lector será eliminar el prefijo var de los parámetros del procedimiento permutar y volver a ejecutar el programa. Podrá observar que los valores no se modifican.
Tipos de Datos
Cuando definimos variables e indicamos que son de un tipo de datos en particular estamos indicando la cantidad de bytes de memoria que se reservará para almacenar los valores que estas variables puedan contener durante la corrida del programa.
Como la cantidad de bytes definida para cada tipo de datos es una cantidad finita resulta que los valores que las variables vayan a contener estarán acotados por estas cantidades finitas de bytes.
Por ejemplo:
El tipo integer implica 2 bytes con bit de signo. Veamos la representación de estos bytes.
Vemos que de los 16 bits que componen los 2 bytes del integer solo se utilizan 15 ya que el más significativo (el primero comenzando desde la izquierda) es el bit de signo. 0 indica que el número representado en estos dos bytes es positivo y 1 indica que el número representado es negativo.
El mayor número que podemos almacenar en una variable de 2 bytes con signo (o sea un integer) es el número binario:
|01111111|11111111|.
Cada bit del número binario representa una potencia de 2. El menos significativo (el más a la derecha) representa la potencia 0 (es decir 2 elevado a la cero) que vale 1. El siguiente (hacia la izquierda) representa la potencia 1 (o sea 2 elevado a la 1) que vale 2 y así.
La conversión entonces surje de sumar los valores representados por los bits del número binario que estén en 1.
b1 = |00000000|00010000| en decimal es 16 ya que solo sumamos el valor representado por el bit que está en 1.
b2 = |00000000|00010001| en decimal es 17. Resulta de sumar los valores representados por los bits en las posiciones 0 y 4, es decir: 2 elevado a la cero + 2 elevado a la 4. Resulta: 1+16 = 17.
Vemos entonces que el mayor número que podemos obtener en 2 bytes con bit de signo (es decir ignorando el bit más a la izquierda) es el número representado por todos unos salvo el de signo.
Luego sumamos las potencias de 2 representadas por todos esos unos (2 a la cero + 2 a la 1 + ...+ 2 a la 15). Esto da: 32767. Este es el mayor número que puede contener una variable de tipo integer. Y el menor será un número binario con todos los bits en 1, incluso el de signo. Estó es -32768.
En reglas generales diremos que en n bits, el mayor número entero decimal que podemos almacenar es (2 a la n) -1.
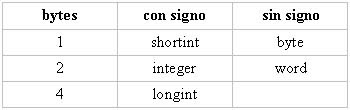
En Pascal podemos utilizar los siguientes tipos de datos:
Numéricos Enteros:
- byte - (1 byte sin signo) - [ 0 , 255 ]
- shortint- (1 byte con signo) - [ -128 , 127 ]
- integer - (2 bytes con signo) - [ -32768 , 32767 ]
- word - (2 bytes sin signo) - [0 , 65535]
- longint - (4 bytes con signo) - [-2147483648 , 2147483647]
Numéricos Reales
- real - (6 bytes) - [1E-38 , 1E+38]
- single - (4 bytes) - [7 dígitos significativos]
- double - (8 bytes) - [15 dígitos significativos]
Alfanuméricos
- string[n] - (n+1 bytes)
- char - (1 byte)
Problema 3.2
Considere dos circunferencias en un plano y un conjunto de 10 puntos. Realizar un programa que indique:
- Cuantos puntos caen dentro de la circunferencia 1
- Cuantos puntos caen dentro de la circunferencia 2
- Cuantos puntos están afuera de la circunferencia 1
- Cuantos puntos están afuera de la circunferencia 2
- Cuantos puntos caen en el centro de la circunferencia 1
- Cuantos puntos caen en el centro de la circunferencia 2
- Cuantos puntos caen dentro de la intersección de las dos circunferencias
- Cuantos puntos caen afuera de las dos circunferencias
Análisis
Veamos un gráfico para poder comprender mejor el problema.
Consideremos la circunferencia 1. Dado un punto (xp, yp) podemos calcular la distancia entre este punto y el punto central de la circunferencia (x1, y1). Luego, si esa distancia es mayor que el radio, el punto estará afuera de la circunferencia. Si la distancia es menor o igual que el radio, el punto estará adentro de la circunferencia. Si la distancia es igual a cero el punto estará en el centro.
Por lo tanto los puntos en cuestión son: (x1, y1) y (xp, yp). La distancia entre esos puntos se puede calcular como:
dist: = sqrt( (xp – x1)2 + (yp – y1)2 )
El problema entonces consiste en leer los 10 puntos, por cada punto calcular la distancia al centro de cada una de las circunferencias y mantener los contadores que correspondan.
Para resolver el problema definimos la funcion procesaCirc. Esta función recibe los datos de una circunferencia (r, x1, y1), los datos de un punto (xp,yp) y retorna un valor negativo o positivo según el punto esté dentro o fuera de la circunferencia.
Además, la función se encarga de incrementar los contadores que correspondan. Por este motivo también recibe el contador de puntos dentro (cCirc1 o cCirc2) el contador de puntos fuera (cFue1 o cFue2) y el contador de puntos en el centro (cCentro1 o cCentro2). Como estos contadores serán incrementados dentro de la función (según corresponda) deben recibirse por referencia (anteponiendo la palabra var) para que la función pueda modificar su valor.
Analizando la función vemos que calcula la distancia (d) entre los dos puntos (cx,cy) y (px,py), y luego evalúa: si d<=r (radio) entonces el punto está dentro de la circunferencia por lo tanto incrementa cDentro. Luego pregunta si d=0 para incrementar cCentro. Si el punto no está adentro entonces estará afuera así que incrementa cFuera.
El valor de retorno de la función debe ser un valor negativo si el punto está adentro o un valor positivo si el punto está afuera de la circunferencia. La diferencia entre la distancia (d) y el radio (r) (negativa si la distancia es menor que el radio y positiva si la distancia es mayor) es el valor de retorno que necesitamos devolver en la función.
Ahora, analizando el programa principal: leemos los 10 puntos (xp, yp) y por cada punto invocamos dos veces a la función procesaCirc. La invocamos con los datos de la circunferencia 1 (r1, x1, y1) y luego la invocamos con los datos de la circunferencia 2 (r2, x2, y2) . Si ambos resultados son negativos entonces el punto está dentro de las dos circunferencias: está en la intersección así que incrementamos cInter. En cambio, si los dos resultados fueron positivos entonces el punto no está dentro de ninguna de las dos circunferencias. Incrementamos cNing.
problema3.2.pas
1:
2:uses math; // una de las librerias de Pascal
3:
4:// desarrollo de la funcion procesaCirc
5:function procesaCirc(
6: r,cx,cy,px,py:real;
7: var cDentro ,cCentro ,cFuera:integer): real;
8:var d:real;
9:begin
10: // la funcion power esta definida en math
11: d:=sqrt( power(px-cx,2) + power(py-cy,2) );
12: if( d<=r ) then begin
13: cDentro:=cDentro+1;
14: if( d=0 ) then begin
15: cCentro:=cCentro+1;
16: end;
17: end else begin
18: cFuera:=cFuera+1;
19: end;
20:
21: procesaCirc:= d-r;
22:end;
23:
24:// programa principal
25:var
26: cCirc1,cCirc2,
27: cCentro1,cCentro2,
28: cFue1,cFue2,cInter,cNing:integer;
29: d1,d2: real;
30: r1,x1,y1,r2,x2,y2: real;
31: xp,yp: real;
32: i: integer;
33:begin
34: cCirc1:=0;
35: cCirc2:=0;
36: cCentro1:=0;
37: cCentro2:=0;
38: cFue1:=0;
39: cFue2:=0;
40: cInter:=0;
41: cNing:=0;
42:
43: write('Ingrese circunferencia 1 (r1,x1,y1): ');
44: readln(r1,x1,y1);
45:
46: write('Ingrese circunferencia 2 (r2,x2,y2): ');
47: readln(r2,x2,y2);
48:
49: for i:=1 to 10 do begin
50:
51: write('Ingrese punto ',i,' (xp,yp): ');
52: readln(xp,yp);
53:
54: d1:=procesaCirc(r1,x1,y1,xp,yp,cCirc1
55: ,cCentro1,cFue1);
56: d2:=procesaCirc(r2,x2,y2,xp,yp,cCirc2
57: ,cCentro2,cFue2);
58:
59: if( (d1<0) AND (d2<0) ) then begin
60: cInter:=cInter+1;
61: end else begin
62: if( (d1>0) AND (d2>0) ) then begin
63: cNing:=cNing+1;
64: end;
65: end;
66: end;
67:
68: writeln('Circunferencia 1: Adentro:',cCirc1
69: ,' Centros:',cCentro1,' Afuera:',cFue1);
70: writeln('Circunferencia 2: Adentro:',cCirc2
71: ,' Centros:',cCentro2,' Afuera:',cFue2);
72: writeln('Interseccion:',cInter
73: ,' Afuera de las dos:',cNing);
74:end.
75:
Argumentos en Línea de Comandos
Muchas veces necesitamos pasarle parámetros (o argumentos) directamente al programa principal. Ejemplos de esto son:
- format C:
- copy archivo1.exe archivo2.exe
- grep "buscando esto" *.pas
En Pascal (y en todos los lenguajes de programación) podemos hacer que nuestros programas reciban este tipo de argumentos. Veamos el siguiente ejemplo.
testArg1.pas
1:
2:var i,n:integer; p:string;
3:begin
4: // obtengo la cantidad de parametros que recibe
5: // el programa principal
6: n := paramCount();
7:
8: writeln('paramCount():',n);
9:
10: // ahora muestro cada uno de esos parametros
11: // identificados por su posicion
12:
13: for i:=1 to n do begin
14: // accedo al parametro 1, luego al 2 y asi...
15: p := paramStr(i);
16: writeln( p );
17: end;
18:end.
19:
Este programa recibe argumentos en línea de comandos, muestra la cantidad de argumentos que recibe y luego muestra cada uno de esos argumentos.
Pascal provee las funciones paramCount y paramStr. La primera retorna la cantidad de parámetros que el programa está recibiendo (ver línea 6). Si no recibió ningún parámetro entonces retorna cero. La segunda recibe el número del parámetro al cual queremos acceder y retorna el parámetro ubicado en dicha posición. Es decir: si queremos leer el valor del primer parámetro le pasamos 1, si queremos leer el valor del segundo parámetro le pasamos 2 y así sucesivamente (ver línea 15).
Luego de compilar este programa podemos ejecutarlo y pasarle parámetros como vemos a continuación.

En la imagen vemos que se invoca al programa testArg1 con los parámetros pablo, analia, jose y marcos. El programa muestra la cantidad de parámetros recibidos (4) y luego muestra cada uno de estos parámetros, uno debajo del otro.
Algoritmos y Estructuras de Datos UTN - UBA..









No hay comentarios:
Publicar un comentario